手続き脳によるHaskell -- ヒープソート(heap sort)

　ここでは、Haskellでヒープソート(heap sort)を実装してみましょう。 ヒープソートを知らない人は このページ の最後のリンクからアップヒープ操作によるヒープソートを参照してください。 このページでは根(root)に最大値が割り当てられるヒープを紹介していますが、 Haskell でヒープソートを実装するには根に最小値が割り当てられる方が 自然なコードが書けるので、 本ページでは根に最小値が割り当てられるヒープで実装します。 アルゴリズムは大小関係が逆転しているだけで 最大値が割り当てられるヒープとほぼ同じです。

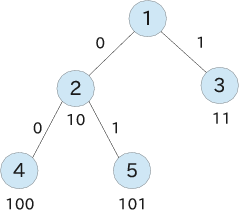
　もう一つ、参照ページと違うところはノード番号の割当です。本ページでは、 根(root)に 1 を割り当てます。そして現在注目しているノード番号を \(k\) とした場合、左の子に \(2k\) 番を、右の子に \(2k + 1\) 番を割り当てることにします。このように割り当てると、 ノード番号のビットパターンが、 根からそのノード番号のノードに至るパスを表すことになります。 左の枝を 0 、右の枝を 1 とすると、 ノード番号の最上位ビットを除いた部分が、そのままパスになっています。

完全２分木のノード番号のビットパターンとパスの関係

　さて、C や Java でヒープソートを実装しようと思ったら、 配列の上に完全２分木を展開することで実現すると思いますが、 Haskell ではそうはいきません。Haskell にも配列はありますが、 原則的に副作用を禁止しているので、配列の部分的書き換えに \(O(n)\) の計算量がかかってしまいます。これではヒープソートの計算量を \(O(n\log n)\) に抑えることができません。

　そこで配列を使わず、直接木構造を扱うことでこの問題を解決します。 ２分木と最大ノード番号の組で完全２分木を表します。以下に Haskell によるヒープソートの実装を示します。

　もはやこれは「普通にやれ、普通に！」 のスローガンにそっているとは言い難いですね。私も流石に言い訳出来ません。 しかし、これで Haskell でも完全２分木を使ったヒープソートが実装可能であることが分かったと思います。実用性を考慮すると Haskell でヒープソートを実装すると言えば、leftist heap や skew heap といった Haskell により適した完全２分木ではない木構造を使います。

　ところで、{-# LANGUAGE BangPatterns #-} というコメントが意味不明かもしれませんが、これは Haskell の遅延評価を出来るだけ回避する仕組みを使うことを宣言しています。 この宣言をした上で関数の引数に(!)を付けると、 その引数が遅延評価されなくなります。また、 let !(x, y) = ... のように書いた場合に通常の let (x, y) = ... より効率が良くなります。

　さらに、data Heap a = Heap !MaxNodeNum !(Tree a) のように、代数データ型のフィールドに(!)を付けると、 この代数データ型が評価されるときに、 そのフィールドが遅延評価されなくなります。こちらは、 BangPatterns の宣言がなくても使えます。

　なにやら(!)ばかりでうっとうしいですが、 このようにするとかなり速くなります。 Haskell ってつくづく面倒くさい言語ですよね(^^;

【追記】

　もう１つ、ユニークなヒープソートの実装を紹介しましょう。 オーム社の「関数プログラミング入門 -- Haskellで学ぶ原理と技法」 で紹介されていた方法を私がアレンジしたものです。

　Haskell でヒープソートというと普通は、 サイズ 0 のヒープから始めて要素を１つ１つ追加して成長させ、 全ての要素を追加したら今度は、 最小値を順々に取り出してヒープを縮めていくという方法でソートします。 　しかし、ここで紹介する実装は非常にユニークで、 fromList 関数で２分木を一挙に作ってしまい、 それをヒープに変換後、toList 関数で マージソート 風にリストにマージすることでソートします。 作られる２分木は完全２分木ではありませんが、ほぼ完全２分木状になります。 こうすると完全２分木を構築するための面倒な仕組みが必要なくなり、 コードが非常に簡単になります。それでは見てみましょう。 以下のようになります。

　ただしこの方法は、純粋にヒープソートするためだけの方法です。 ヒープの重要な応用であるところの、優先度付きキューの実装には使えません。 しかし、Haskell でヒープソートってどうやって実装するんだ？ と疑問に感じている人にとっては、 目から鱗の解決策になるのではないでしょうか。

　ところで、この実装の fromList 関数・makeTree 関数には、 マージソート のところで解説したタプリングの技法が用いられています。 タプリングを用いると、何と２分木の生成が \(O(n)\) の計算量で完了します。 タプリングを用いずにこれらを書き直せば以下のようになるでしょう。

        fromList xs = makeTree (length xs) xs
        makeTree _ []     = Empty
        makeTree n (x:xs) = Node x (makeTree m lhs) (makeTree (n - m - 1) rhs)
            where
                m = n `div` 2
                (lhs, rhs) = splitAt m xs