ツリーソート(2分木ソート, tree sort) は要素の種類が少ないとき、 計算量が \(O(n)\) と高速ですが、ソート済みの系列に適用すると最悪計算量が \(O(n^2)\) と猛烈に遅くなってしまいます。何とか最悪時でも \(O(n\log n)\) 程度に抑える方法はないでしょうか?実はあります。 バケツ(要素を保存するリスト)を配置する2分探索木で常に平衡を保つようにしてやれば良いのです。 そうした平衡木のアルゴリズムの一つが赤黒木(2色木、red-black tree)です。
ここでは、Haskell で赤黒木を使ったツリーソートを実装してみましょう。 もちろん、赤黒木を使ったツリーソートも安定ソートです。 Haskell による赤黒木を使ったツリーソートの実装は以下のようになります。
赤黒木は以下の条件を満たした2分探索木です。 葉の定義がちょっと変わっていますので注意してください。
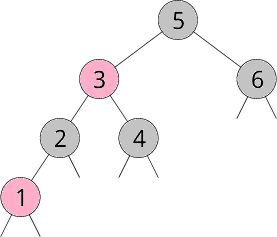
下図の赤黒木の例で説明すると、ノードとは数字の入っている丸のことです。 根 (root) とは最上位のノードのことです。図では5のノードです。 各ノードから出ている下の線を枝と言います。 子とは注目しているノードから見て枝をたどって直下のノードのことです。 子から見て元のノードを親と言います。 葉 (Leaf) とは各ノードの子を持たない枝のことです。 各ノードを根とみなした木のことを部分木と言います。 注目しているノードに対して、左の子を根とみなした部分木を左部分木、 右の子を根とみなした部分木を右部分木と言います。 最大の部分木は赤黒木自身です。

|
上記の条件により、あり得る最も短いパスは黒いノードのみを含み、 あり得る最も長いパスには赤と黒が交互に現れることになります。 つまり赤黒木は、 大まかに言って最長のパスの長さが最短のパスの長さの2倍以内に収まる平衡木ということになります。
赤黒木を作るには上記のコードの insertBy 関数を使います。
新しいノードは赤で追加します。もし新しいノードが根なら、
問答無用で黒に変更して処理終了です。
黒の子として赤のノードを追加した場合は、
赤黒木の条件は崩れませんのでそのままで処理終了です。
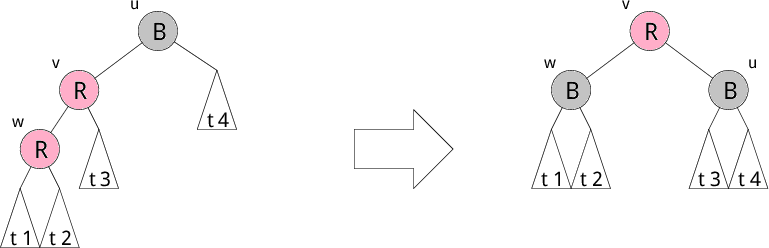
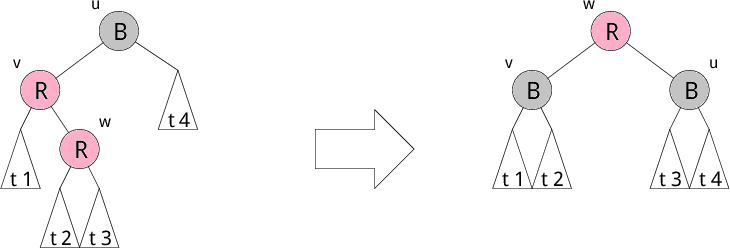
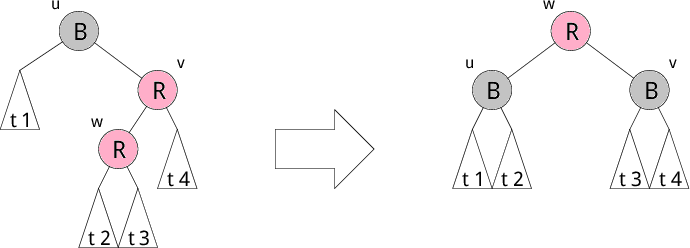
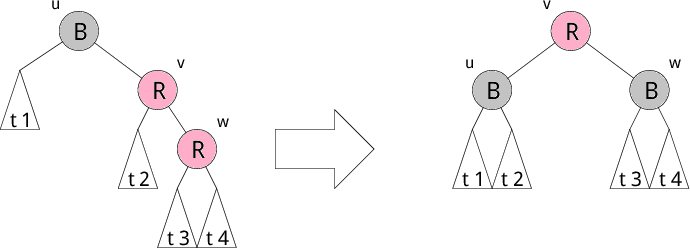
赤の子として赤のノードを追加すると、条件3が満たされなくなります。 そこで、 回転という操作で木を変形し色を変更して条件3が成り立つように修正します。 赤の子として赤のノードを追加する部分木のパターンは、 以下で示す4つのパターンがあります。 それぞれ左図を右図の木のように修正します。修正後、 葉から根へのパス上の黒ノードの個数が変わらないところが重要です。 これで条件4が守られます。もちろん、2分探索木の条件も崩れていません。
以下にそれぞれのパターンを示します。R が赤、B が黒を表しています。 t1,t2,t3,t4 などの部分木は葉 (Leaf) になることもあります。
|
|
|
|
現在注目している部分木を修正した結果、 上位の階層(根に近い階層)で赤黒木の条件3が崩れる可能性があります。 その場合、根に到達するまで上位階層で木の修正を繰り返します。 根に到達して根が赤になった場合、問答無用で黒に変更します。 このとき全てのパス上で黒ノードの個数が1つ増えることになります。
さて、赤黒木と言えばソートに使うというより、 マップを実装するデータ構造として有名です。 せっかく赤黒木を使ったのですから、面倒なことで知られる delete の処理も含んだマップの実装も見てみましょう。以下のようになります。 Java による実装をお望みの方は こちらのページ へどうぞ。
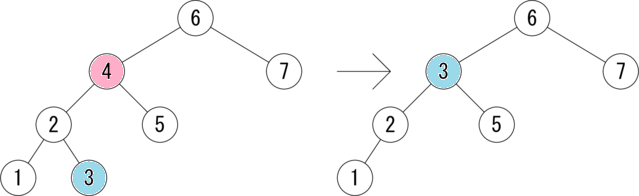
赤黒木の削除を説明する前に、2分探索木の削除について簡単に説明します。 2分探索木でノードの削除を行うには、 削除したいノードが左端のノードの場合は、単にそのノードを削除し、 そのノードに右部分木があったのならそれを昇格させます。 また、削除したいノードが左部分木を持つ場合は、 左部分木の最大値のノードで削除したいノードを置き換え、 最大値だったノードを削除します。このとき、 削除したノードに左部分木があったのならそれを昇格させます。 以下に、2分探索木の削除の一例を具体的に示します。
|
図は、赤で示した 4 を削除する例を示しています。 4 には左部分木があります。そして、 4 の左部分木の最大値は 3 ですので、 4 を 3 で置き換え、元の 3 を削除します。 削除後も2分探索木の大小関係がうまく保たれていることが分かると思います。
赤黒木の場合、削除操作は2分探索木の削除操作に加えて、 赤黒木の条件を崩さないように修正する必要があります。
赤ノードの削除は赤黒木の条件を崩さないので、修正する必要はありません。
しかし、黒ノードを削除すると、
葉から根へのパス上の黒ノード個数が1つ減り、条件4が崩れますので、
修正が必要になります。修正の必要性を示す Change フラグを
True にして木を根の方向にさかのぼります。そして、
パターンマッチで修正パターンを見つけて修正を行います。修正後、
さらなる修正が必要な場合、フラグを True
にしてさかのぼります。修正が必要なくなったら フラグを False
にしてさかのぼります。
一度フラグを False にすると、それ以上は修正しません。
そして、根までさかのぼったら修正完了です。
このとき、根の色が赤になった場合は問答無用で黒に変更します。
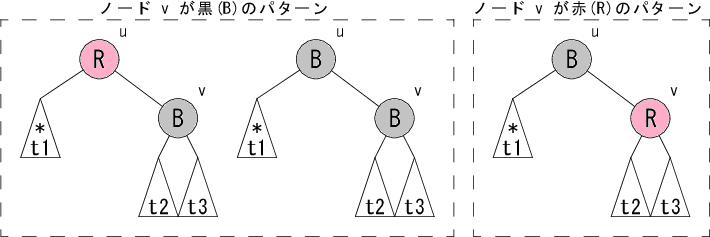
黒ノードの削除に伴う修正を具体的に説明しましょう。今、左部分木の t1 で黒ノード個数が減ったとして、あり得る部分木のパターンを示すと、 大まかに以下の3パターンになります。u, v がともに赤のパターンは、 赤黒木の条件により存在しないことに注意してください。
|
アスタリスク(*)が黒ノードが減ったことを表してします。 始めに大分類としてノード v が何色かで分類します。
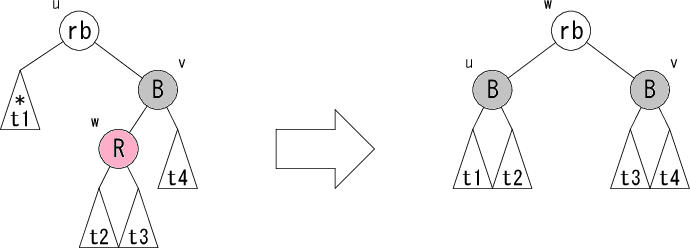
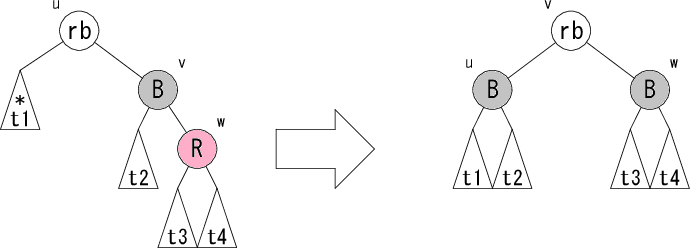
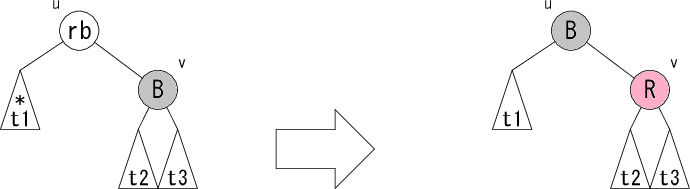
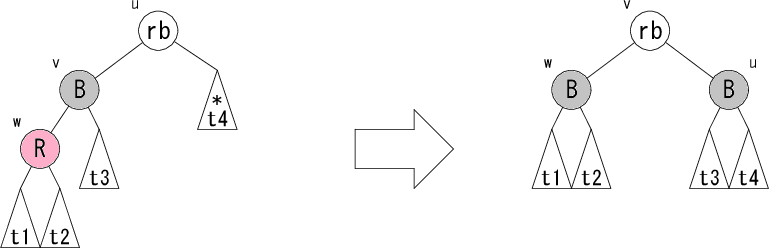
次に、ノード v が黒の場合の修正パターンの詳細を見てみましょう。 以下のようなパターンが考えられます。
|
|
|
rb は赤か黒のどちらかです。修正前が赤なら修正後も赤、
修正前が黒なら修正後も黒です。パターンL1,L2 の修正後の右図では、部分木
t1 から根へのパス上に黒ノードが1つ増えるので、条件4が回復します。
これ以上修正は必要ないので、Change フラグを
False にして木をさかのぼります。
パターンL3 はパターンL1 とパターンL2
にマッチしなかった残りにマッチするパターンです。
これでノード v が黒の場合は全て網羅されます。
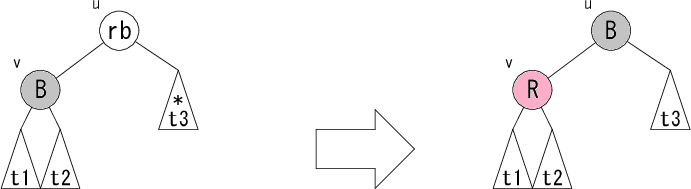
パターンL1,L2 にマッチしなかったので、部分木 t2,t3
は葉になるか根が必ず黒になります。
そのため、ノード v を赤にしても赤黒木の条件3は崩れません。
rb が赤だった場合は条件4が回復しますので、Change
フラグを False にして木をさかのぼります。
rb が黒だった場合、ノード u
を根とする部分木全体で根へのパス上の黒ノード個数が1つ減りますので修正が必要です。
Change フラグを True
にして木をさかのぼります。
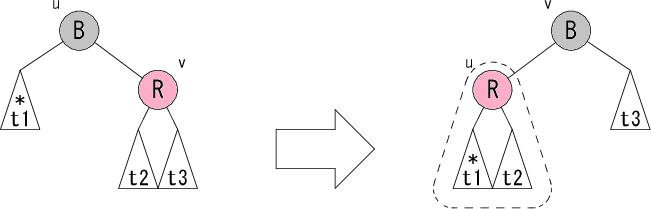
|
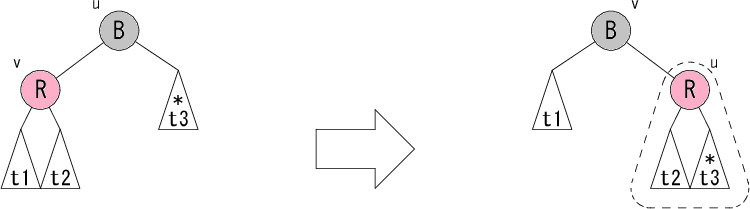
最後はノード v が赤のパターンL4 です。ノード u が黒でノード v が赤ですから、赤黒木の条件より、部分木 t2 の根は必ず黒いノードになります。 そこで右図のように修正すると、 点線で囲んだ部分木が上記のパターンL1,L2,L3 に当てはまります。 後は点線で囲んだ部分木に再帰的に修正パターンを適用すれば、 木全体の修正が行えることになります。 部分木 t1 の根の色が赤になる場合、一時的に赤黒木の条件3が崩れますが、 修正後の親ノードの色が黒になるので大丈夫です。
修正に再帰を使ったので、
再帰的修正が際限なく繰り返されるのではないかと心配する人も居るかもしれませんが、
再帰的修正を行うパターンはL4のみです。
点線で囲った部分木に適用するパターンはL1,L2,L3ですので、
再帰が再び再帰する心配はありません。必ず1段で終了します。修正により、
条件4が回復しますので Change フラグを False
にして木をさかのぼります。
これで左部分木の黒ノード個数が減った場合の修正パターンは完了です。 残るは右部分木の黒ノード個数が減った場合ですが、 これは左右対称なパターンとなっていますので説明は省略します。 コーディングの助けのために図だけ示すこととします。
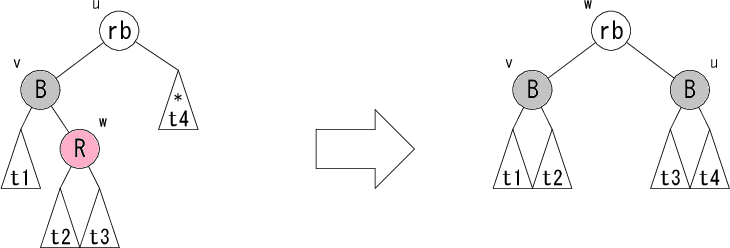
|
|
|
|
如何でしょう?面倒なことで有名な赤黒木の delete ですが、 結構簡単に実装出来ていますよね。実は私も、 Web を見ながら赤黒木の勉強をしたのですが、 どのページを見ても delete の説明がピンときませんでした。 パターンがやたらと多いのが原因の1つです。 仕方が無いので delete に関しては、自分で一から考えました。 その結果がこのページです。対称なパターンを省けば、 実質的なパターンは4パターンに収まっています。 これなら何とか記憶できる分量ですよね。
自分で考えたのでひょっとすると間違いや漏れがあるかもしれません。 このページを参考にする人は、その辺を考慮して自己責任でお願いします。