赤黒木
【これで分かった赤黒木】
このページは、 マップ(連想配列)と呼ばれるデータ構造の実装の1つである赤黒木(2色木、red-black tree)について解説するページです。 赤黒木は、要素の挿入・削除・検索などの操作が、 いかなる場合でも O(log n) の計算量で実行出来る平衡2分探索木です(n は要素数)。 何の工夫もしない単なる2分探索木では、 挿入や削除のパターンによっては木の茂り方のバランスが崩れてしまい、 各種操作に O(n) の計算量が必要になる場合があります。 赤黒木はやっていることは単純なのですが、 とにかく場合分けがたくさんあって、 習得しようとしながらもくじけてしまった人も多いのではないでしょうか?
しかし、ご安心ください。このページは場合分けを出来るだけ減らし、 挿入操作で4パターン、 削除操作で8パターンさえ理解すれば赤黒木が分かるように書かれています。 削除操作に関しては、 左右対称のパターンを省けば4パターン理解すればおおむね OK です。 これから赤黒木を勉強しようという人はもちろん、 一度は勉強したが挫折してしまったという人も是非とも読んでみてください。 サンプルコードは こちら です。
赤黒木より実装が簡単な平衡木であるAVL木について興味のある人は、 こちらのページ をご覧ください。ファイルシステムやデータベースの基盤技術であるB木について興味のある人は、 こちらのページ をご覧ください。 B木の最も簡単なケースである2-3木について興味のある人は、 こちらのページ をご覧ください。 赤黒木の簡略版である Left-Leaning Red-Black Tree について興味のある人は、 こちらのページ をご覧ください。
【準備】
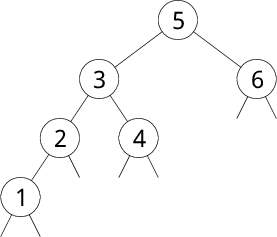
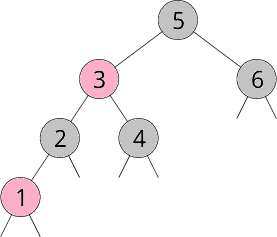
まず、準備から始めましょう。赤黒木は2分探索木の一種です。 2分探索木 というのは以下のようなグラフ(木)のことです。以下で、 用語をいくつか定義します。
|
数字を丸で囲んでいるものをノードと言います。 ノードから出ている下側の 2本の線を枝と言います。 枝の先にあるノードのことを元のノードに対して子と 言います。 子から見ると、 元のノードを親と言います。親子関係で最上位のノードことを根 (root) と言い、子を持たない枝のことを葉と言います。図1 では 5 が根です。 注目しているノードの左の子を根と見なした木のことを左部分木と言い、 右の子を根と見なした木のことを右部分木と言います。
2分探索木とは、 ノードに割り当てられている値が以下の条件を満たしている木のことです。
- 左部分木のノードの値は全て注目しているノードの値より小さい
- 右部分木のノードの値は全て注目しているノードの値より大きい
図1.を見れば、上記の条件が成立していることが分かると思います。 この条件のお陰で、2分探索木は効率的に要素の探索が行えます。例えば図1. で、4 が含まれているかどうかチェックしたければ、まず根から探し始めます。 4 は 5 より小さいので、4 は左部分木に含まれているはずです。 そこで次に 3 を調べます。4 は 3 より大きいので、 4 は右部分木に含まれているはずです。このようにしてついには 4 にたどり着きます。もちろん、 葉までたどり着いて目的の値が見つからない場合もあります。 そのときは、その2分探索木に目的の値は含まれていないことが分かります。
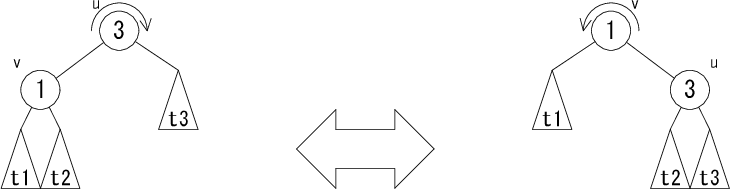
次に、回転について説明します。 回転とは2分探索木の条件を崩さないように木を変形する操作のことです。 具体的には次の図のようになります。三角形は部分木を表しています。
|
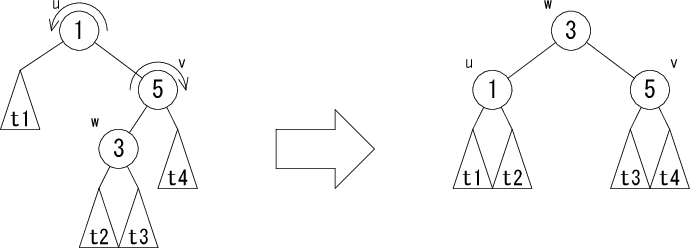
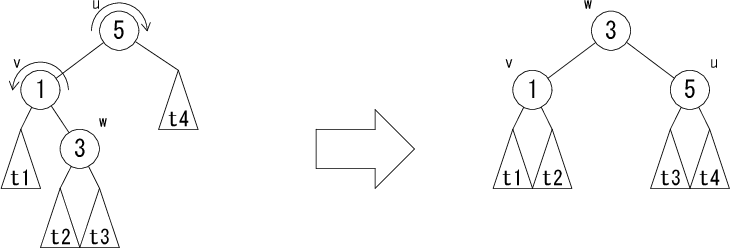
左図の木を右図の木に変形する操作のことを右回転( rotateR(u) )、 右図の木を左図の木に変形する操作のことを左回転( rotateL(v) )と言います。 赤黒木では、この回転を使って木を変形し、 挿入や削除によりバランスの崩れた木の平衡を回復します。回転には、 さらに以下のような2重回転もあります。 まずノード v で回転させてからノード u で回転させます。
|
|
図3 の2重回転を rotateRL(u)、図4 の2重回転を rotateLR(u) と表します。
【赤黒木の定義】
さて、それではいよいよ赤黒木の条件を見てみましょう。 赤黒木とは、以下の条件を満たす2分探索木です。
- ノードは赤か黒である
- 根は黒である
- 赤いノードの子は黒である
- 全ての葉から根へのパス上には、同じ個数の黒いノードがある
|
上記の条件により、あり得る最も短いパスは黒いノードのみを含み、 あり得る最も長いパスには赤と黒が交互に現れることになります。 つまり赤黒木は、大まかに言って最長のパスの長さが最短のパスの長さの2倍以内に収まる平衡木ということになります。
ここで、赤黒木の高さが赤黒木が含むノード数 \(n\) の対数に比例することを確認しましょう。今、部分木 \(x\) の根から葉のパスに含まれる黒いノードの数を黒高さと呼び \(bh(x)\) で表します。赤黒木の性質よりこれは一意に決まります。 始めに、部分木 \(x\) が少なくとも \(2^{bh(x)}-1\) 個のノードを含むことを数学的帰納法で証明します。
まず、\(bh(x)=0\) のとき、すなわち部分木が空か赤ノード1個の場合、 \(2^0-1=0\) であり少なくとも0個のノードを含むことになり、 仮定は成り立ちます。 次に仮定より、黒高さが \(b\) の部分木が少なくとも \(2^b-1\) 個のノードを含むとします。 部分木 \(x\) の根が黒の場合、 \(x\) の左部分木と右部分木はそれぞれ少なくとも \(2^{bh(x)-1}-1\) 個のノードを含みます。 部分木 \(x\) の根が赤の場合、 \(x\) の左部分木と右部分木はそれぞれ少なくとも \(2^{bh(x)}-1\) 個のノードを含みます。 よって少ない方を取って、部分木 \(x\) の左部分木と右部分木は少なくとも \(2^{bh(x)-1}-1\) 個のノードを含むことになります。 したがって、部分木 \(x\) が含むノードの数は少なくとも \(2^{bh(x)-1}-1+2^{bh(x)-1}-1+1=2^{bh(x)}-1\) となり、\(x\) の左部分木と右部分木で帰納法の仮定が成り立つならば、 \(x\) においても帰納法の仮定が成り立つことが証明されました。 すなわち、全ての部分木で帰納法の仮定が成り立ちます。
最後に、赤黒木の性質より、 赤黒木自身の黒高さは少なくとも木の高さ \(h\) の半分になります。 したがって、赤黒木が含むノードの数 \(n\) は少なくとも \(n \ge 2^{(h/2)}-1\) となり、高さ \(h\) は \(h \le 2\log_2(n+1)\) の関係を満たすことになります。 つまり、赤黒木の最悪時の高さ \(h\) はノード数 \(n\) の対数に比例します。
ちなみに、AVL木は高さがおよそ \(1.44\log_2(n+1)\) に比例するので、 赤黒木はAVL木よりバランスが崩れていることになります。 また、完全2分木の高さは \(\log_2(n+1)\) に比例するので、 最悪時の赤黒木は、 理想的なケースに比べると2倍ほど高さが高いということになります。
【挿入操作】
それでは挿入操作 (insert) について説明しましょう。2分探索木では、 要素を挿入するとき、まずは挿入したい値で探索を行います。 そしてもし葉までたどり着いたら、そこに新しくノードを追加します。 もし既に同じ値のノードがあるなら上書きします。
赤黒木では、新しいノードは赤で追加します。もし新しいノードが根なら、 問答無用で黒に変更して処理終了です。 黒の子として赤のノードを追加した場合は、 赤黒木の条件は崩れませんのでそのままで処理終了です。
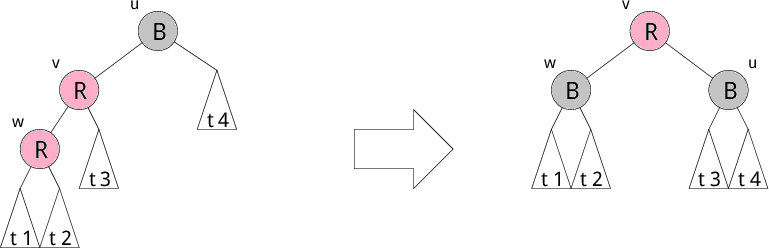
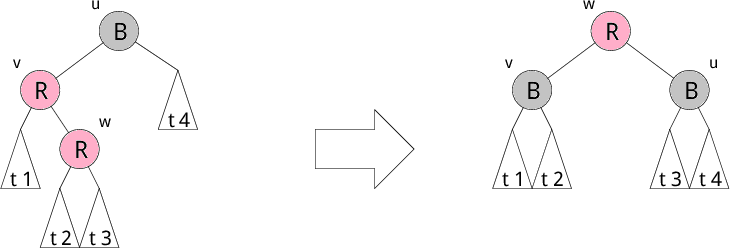
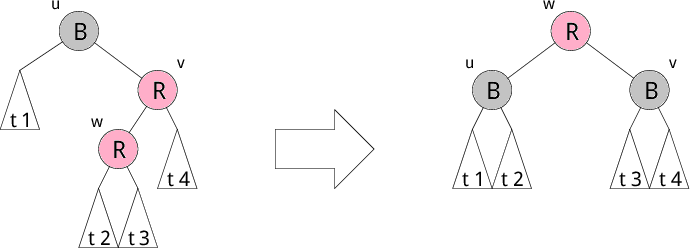
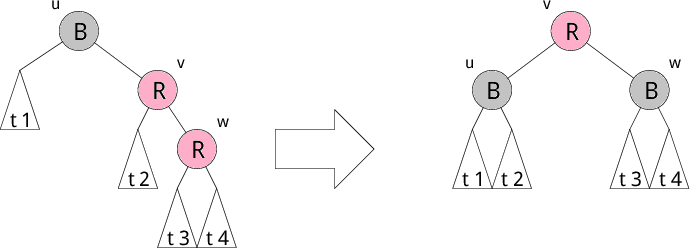
赤の子として赤のノードを追加すると、条件3が満たされなくなります。 そこで、修正中であることを示す active フラグを True にして修正を始めます。 そして、回転で木を変形し色を変更して条件3が成り立つように修正します。 赤の子として赤のノードを挿入する部分木のパターンは以下で示す4つのパターンがあります。それぞれ左図を右図の木のように修正します。 修正後、葉から根へのパス上の黒ノードの個数が変わらないところが重要です。 これで条件4が守られます。もちろん、2分探索木の条件も崩れていません。
以下にそれぞれのパターンを示します。R が赤、B が黒を表しています。 t1,t2,t3,t4 などの部分木は葉になることもあります。 注目している部分木の根 u の色が黒でない場合は、 修正しないでそのまま上位の木へさかのぼります。 その際、active フラグは変更しません。
|
|
|
|
左図のパターンにマッチした場合、 現在注目している部分木を右図のように修正します。その結果、 上位の階層(根に近い階層)で赤黒木の条件3が崩れる可能性があります。 その場合、根に到達するまで上位階層で木の修正を繰り返します。 それ以外の場合は、active フラグを False にしてさかのぼります。 一度 active フラグを False にするとそれ以上は修正を行いません。 そして、根に到達して根が赤になった場合、問答無用で黒に変更します。 このとき全てのパス上で黒ノードの個数が1つ増えることになります。
これらの処理は、サンプルコードでは _balance
で行われている処理です。
【削除操作】
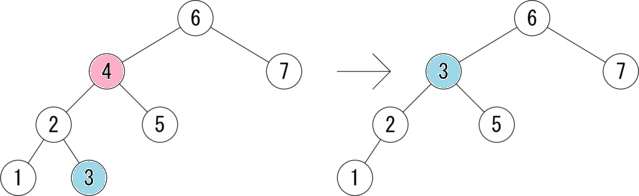
次に、削除操作 (delete) について説明しましょう。ただし、 赤黒木の削除を説明する前に、2分探索木の削除について簡単に説明します。 2分探索木でノードの削除を行うには、 削除したいノードが左端のノードの場合は、単にそのノードを削除し、 そのノードに右部分木があったのならそれを昇格させます。 また、削除したいノードが左部分木を持つ場合は、 左部分木の最大値のノードで削除したいノードを置き換え、 最大値だったノードを削除します。このとき、 削除したノードに左部分木があったのならそれを昇格させます。 以下に、2分探索木の削除の一例を具体的に示します。
|
図は、赤で示した 4 を削除する例を示しています。 4 には左部分木があります。そして、 4 の左部分木の最大値は 3 ですので、 4 を 3 で置き換え、元の 3 を削除します。 削除後も2分探索木の大小関係がうまく保たれていることが分かると思います。
赤黒木の場合、削除操作は2分探索木の削除操作に加えて、 赤黒木の条件を崩さないように修正する必要があります。
赤ノードの削除は赤黒木の条件を崩さないので、修正する必要はありません。
しかし、黒ノードを削除すると、
葉から根へのパス上の黒ノード個数が1つ減り、条件4が崩れますので、
修正が必要になります。
修正中であることを示す active フラグを
True にして木を根の方向にさかのぼります。そして、
パターンマッチで修正パターンを見つけて修正を行います。修正後、
さらなる修正が必要な場合、フラグを True
にしてさかのぼります。修正が必要なくなったら フラグを False
にしてさかのぼります。一度フラグを False にすると、
それ以上は修正しません。そして、根までさかのぼったら修正完了です。
削除時の修正パターンでは根は必ず黒になるので、
根の色を修正する必要はありません。
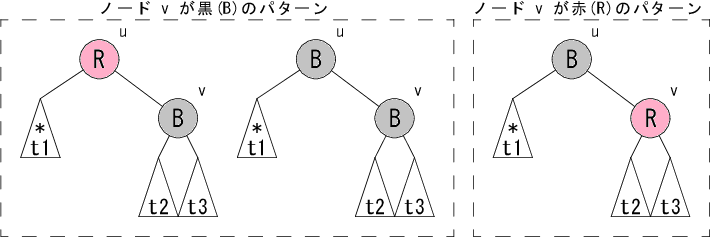
黒ノードの削除を具体的に説明しましょう。今、左部分木の t1 で黒ノード個数が減ったとして、あり得る部分木のパターンを示すと、 大まかに以下の3パターンになります。 u, v がともに赤のパターンは赤黒木の条件により存在しないことに注意してください。
|
アスタリスク(*)が黒ノードが減ったことを表してします。 始めに大分類としてノード v が何色かで分類します。
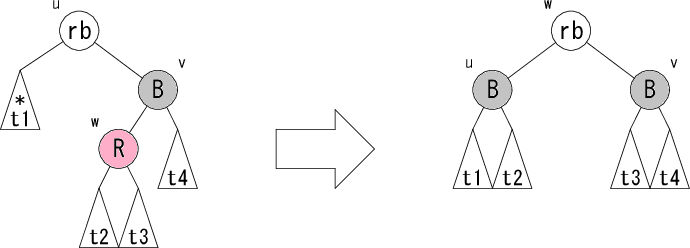
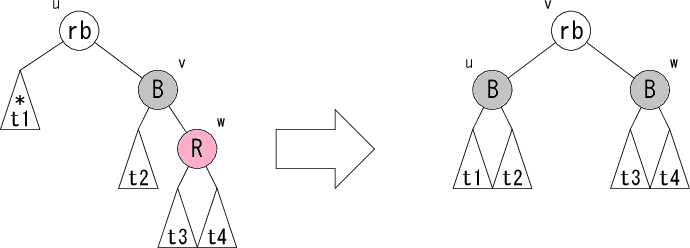
次に、ノード v が黒の場合の修正パターンの詳細を見てみましょう。 以下のようなパターンが考えられます。
|
|
|
修正前が左図、修正後が右図です。rb は赤か黒のどちらかです。
修正前が赤なら修正後も赤、
修正前が黒なら修正後も黒です。パターン L1,L2 の修正後の右図では、
部分木 t1 から根へのパス上に黒ノードが1つ増えるので、
条件4が回復します。これ以上修正は必要ないので、active
フラグを False にして木をさかのぼります。
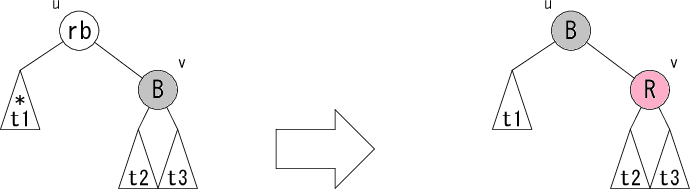
パターン L3 はパターン L1 とパターン L2 にマッチしなかった残りにマッチするパターンです。これでノード v が黒の場合は全て網羅されます。
パターン L1,L2 にマッチしなかったので、
部分木 t2,t3 は葉になるか根が必ず黒になります。
そのため、ノード u を黒ノード v を赤にしても赤黒木の条件3は崩れません。
rb が赤だった場合は条件4が回復しますので、active
フラグを False にして木をさかのぼります。
rb が黒だった場合、ノード u を根とする部分木全体で根へのパス上の黒ノード個数が1つ減りますので修正が必要です。active
フラグを True にして木をさかのぼります。
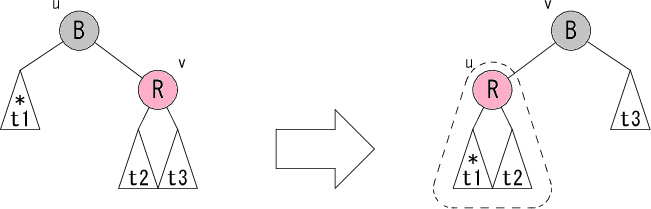
|
最後はノード v が赤のパターン L4 です。ノード u が黒でノード v が赤ですから、赤黒木の条件より、 部分木 t2 の根は必ず黒いノードになります。そこで右図のように修正すると、 点線で囲んだ部分木が上記のパターン L1,L2,L3 に当てはまります。 後は点線で囲んだ部分木に再帰的に修正パターンを適用すれば、 木全体の修正が行えることになります。 部分木 t1 の根の色が赤の場合、一時的に赤黒木の条件3が崩れますが、 修正後の親ノードの色が黒になるので大丈夫です。
修正に再帰を使ったので、
再帰的修正が際限なく繰り返されるのではないかと心配する人も居るかもしれませんが、
再帰的修正を行うパターンは L4 のみです。
点線で囲った部分木に適用するパターンは L1,L2,L3 ですので、
再帰が再び再帰する心配はありません。必ず1段で終了します。修正により、
条件4が回復しますので active フラグを False
にして木をさかのぼります。
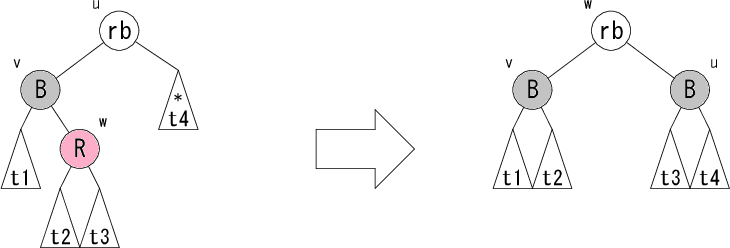
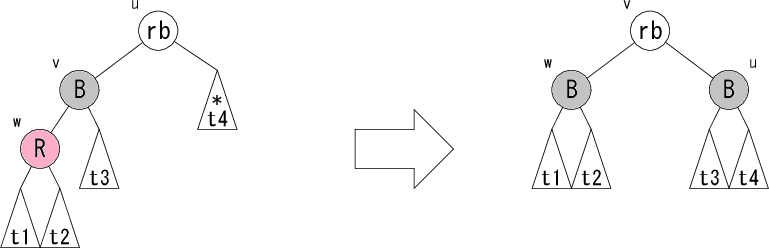
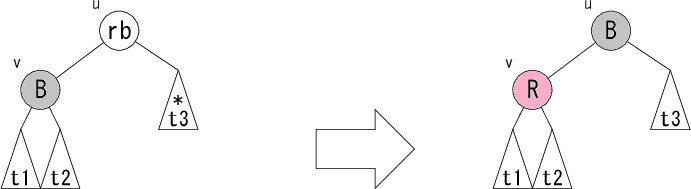
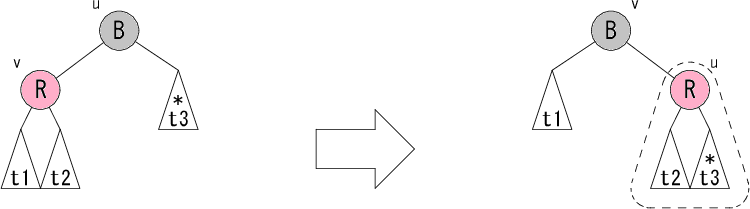
これで左部分木の黒ノード個数が減った場合の修正パターンは完了です。 残るは右部分木の黒ノード個数が減った場合ですが、 これは左右対称なパターンとなっていますので説明は省略します。 コーディングの助けのために以下に図だけ示すこととします。
これらの処理は、サンプルコードでは _balanceL, _balanceR
で行われている処理です。
【コーディングの参考のための図】
|
|
|
|
ところで、このページでも図が多用されていますが、 木のアルゴリズムの説明には図が欠かせません。 そこで、そのような図を描くためのツールを作りました。 興味のある方は、 こちらのページ をご覧ください。
【サンプルコード】
以下に、Java と Python による赤黒木のサンプルコードを示します。 タブになっていますので、目的の言語を選んでください。 このサンプルコード、パターンマッチの分かりやすさを優先したため非効率な記述になっている箇所があります。 極限まで効率を追求する人は自分で修正してくださいね。
【あとがき】
このページは、私自身が Web で赤黒木を勉強した経験から生まれました。 赤黒木の挿入操作に関しては納得出来る簡単なページもあったのですが、 削除操作に関してはどのページも理解できませんでした。仕方が無いので、 削除に関しては自分で一から考えました。どうでしょう、 皆さんには分かりやすかったでしょうか? このページが少しでも皆さんの赤黒木の理解の助けになれば、 筆者の何よりの喜びです。
ところで、他のサイトで赤黒木を勉強した人は、 本サイトの赤黒木の挿入のところで違和感を覚えたかもしれません。 もっと複雑だったはずだけどと思ったことでしょう。 近代科学社のアルゴリズムイントロダクションなどでは、 挿入の場合分けが4パターンではなく6パターンの方法が紹介されています。 しかも、再帰は使わず、 ノードに親を指すリンクを追加してループで実装されています。 これにはわけがあります。4パターンの方法は 6パターンの方法よりも遅いのです。たぶん効率を優先した結果、 6パターンの方法が採用されているのでしょう。
しかし、6パターンの方法は、 木の親子関係で叔父(親の兄弟)まで持ち出してパターンマッチします。 既に赤黒木を十分理解した人なら叔父を持ち出す理由が理解できるので、 それほど難しいとは感じないかもしれませんが、 赤黒木の初学者には非常にミステリアスに感じられるのではないでしょうか? そんなわけで、 本サイトでは分かりやすさを優先して4パターンの方法を採用しました。 高速な赤黒木を目指す人は、4パターンの方法を十分に理解してから 6パターンの方法に挑戦してみてください。たぶん、あれっ? こんなに簡単だったっけと感じると思いますよ(^^;