AVL木
【これで分かったAVL木】
AVL木(AVL Tree)は、 マップ(連想配列)と呼ばれるデータ構造の実装に使われる平衡2分探索木の1つです。 平衡2分探索木では木のバランスが適度にとれており、 キーの検索・要素の挿入・削除などの処理が、いかなる場合でも O(log n) の計算量で行えます(n は要素数)。 何の工夫もしない単なる2分探索木では、 挿入や削除のパターンによっては木の茂り方のバランスが崩れてしまい、 各種操作に O(n) の計算量が必要になる場合があります。
AVL木の他にも 赤黒木 という平衡2分探索木がありますが、 AVL木は赤黒木に比べてより厳密に平衡性を維持しようとします。つまり、 よりバランスがとれているということです。 そのため赤黒木より検索の性能が良いとされています。
かつては、挿入や削除の性能は、 AVL木より赤黒木の方が良いとされていました。しかし、 私の実装したアルゴリズムでベンチマークする限り、 Java では、挿入や削除の性能もAVL木の方が優れているようです。 時代によって、CPU やメモリの性能のバランスは変化しているので、 今はAVL木の方が総合的にも性能が良いようです。 しかし、Python の場合は赤黒木の方が性能が良いようです。
本ページは、AVL木の実装に関して詳しく解説しています。 他のサイトでは省略されてしまっているような回転の場合分けについてもやさしく解説してあります。 その他にも、何故そうするの?という疑問に対して、 なるたけ答えるように書いたつもりですので、是非ともご一読ください。 サンプルコードは こちら です。
ファイルシステムやデータベースの基盤技術であるB木について興味のある人は、 こちらのページ をご覧ください。 また、B木の最も簡単なケースである2-3木に興味のある人は、 こちらのページ をご覧ください。 より高速な、Java による再帰を使わないAVL木の実装に興味のある人は、 こちらのページ をご覧ください。
【準備】
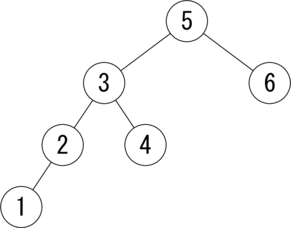
まず、準備から始めましょう。AVL木は2分探索木の一種です。 2分探索木というのは以下のようなグラフ(木)のことです。以下で、 用語をいくつか定義します。
|
数字を丸で囲んでいるものをノードと言います。 ノードから出ている下側の2本の線を枝と言います。 枝の先にあるノードのことを元のノードに対して子と言います。 子から見ると、元のノードを親と言います。 親子関係で最上位のノードことを根(root)と言い、 木の最下層の末端のノードのことを葉(leaf)と言います。 図1.では 5 が根です。
特定のノードを根と見なした場合の木のことを部分木と言います。 注目しているノードの左の子を根と見なした木のことを左部分木と言い、 右の子を根と見なした木のことを右部分木と言います。 最大の部分木とはすなわち木全体のことです。
部分木の根から葉までのノード数の最大値を、その部分木の高さと言います。 ただし、空の部分木の高さは 0 とします。 図1.で見ると、根5 から葉1 までのノード数が 4、 根5 から葉4 までのノード数が 3、 根5 から葉6 までのノード数が 2 ですから、 ノード数の最大値 4 が木の高さになります。
2分探索木とは、 ノードに割り当てられている値が以下の条件を満たしている木のことです。
- 左部分木のノードの値は全て注目しているノードの値より小さい
- 右部分木のノードの値は全て注目しているノードの値より大きい
図1.を見れば、上記の条件が成立していることが分かると思います。 この条件のお陰で、2分探索木は効率的に要素の探索が行えます。 例えば図1.で、4 が含まれているかどうかチェックしたければ、 まず根から探し始めます。 4 は 5 より小さいので、4 は左部分木に含まれているはずです。 そこで次に 3 を調べます。4 は 3 より大きいので、 4 は右部分木に含まれているはずです。このようにしてついには 4 にたどり着きます。もちろん、目的の値が見つからない場合もあります。 そのときは、その2分探索木に目的の値は含まれていないことが分かります。
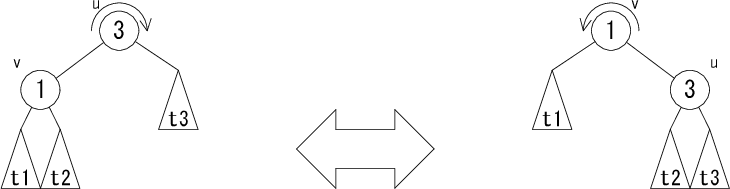
次に、回転について説明します。 回転とは2分探索木の条件を崩さないように木を変形する操作のことです。 具体的には次の図のようになります。三角形は部分木を表しています。
|
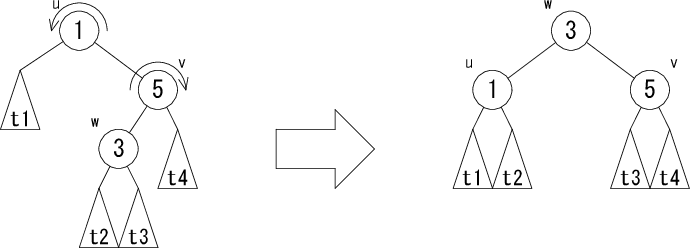
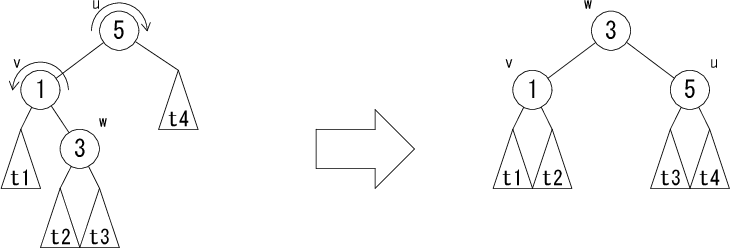
左図の木を右図の木に変形する操作のことを右回転( rotateR(u) )、 右図の木を左図の木に変形する操作のことを左回転( rotateL(v) )と言います。 AVL木では、この回転を使って木を変形し、 挿入や削除によりバランスの崩れた木のバランスを回復します。回転には、 さらに以下のような2重回転もあります。 まずノード v で回転させてからノード u で回転させます。
|
|
図3.の2重回転を rotateRL(u)、 図4.の2重回転を rotateLR(u) と表します。
【AVL木の定義】
それではいよいよAVL木がどんなものか見てみましょう。 AVL木は、バイアスという量で定義されます。 木 t の 高さ を |t| と表すと、バイアスは、
- bias(t) = |t の左部分木| - |t の右部分木|
で定義されます。つまり、バイアスとは左右の部分木の高さの差です。 左部分木が高いと正の値となり、右部分木の高さが高いと負の値になります。
AVL木とは、以下の条件を満たす2分探索木です。
- 2分探索木のあらゆる空でない部分木 t で -1 ≦ bias(t) ≦ 1
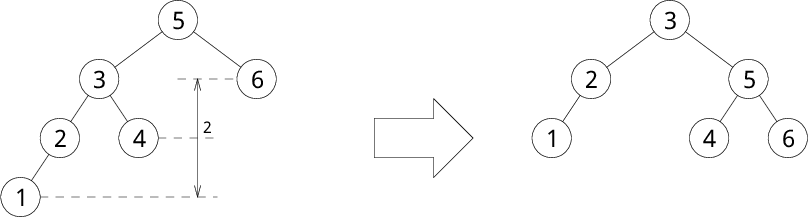
もしバランスが崩れて左右の高さの差が2になったら、 木を回転で変形して再び高さの差が1以内になるように修正します。 具体的には以下のようになります。
|
回転により、 左右の部分木の高さの差は1以内になりバランスが復活します。 そして、2分探索木の各ノードの大小関係も、 うまく保たれていることが分かると思います。
ここで、AVL木の高さがAVL木が含むノード数 \(n\) の対数に比例することを確認しましょう。ノード数が同じなら、 バランスの崩れているAVL木の方が高さは高くなります。 高さは低い方が良いので、最悪の場合を考えて、 同じ要素数でも高さが最も高い場合を考えます。 つまり、最もバランスが崩れているAVL木の高さを考えます。 このとき、高さが \(0\) および \(1\) の部分木を除く全ての部分木で、 その左部分木と右部分木の高さの差が \(1\) になりますから、 \(f(h)\) を高さが \(h\) の部分木が含むノード数の最小値とした場合、 \(f(h+2)=f(h+1)+f(h)+1\) の関係を満たすことになります。 この関係は、\(f(h)=F(h)-1\) と置くと \(F(h+2)=F(h+1)+F(h)\) であり、 \(F(h)\) はフィボナッチ数列になることが分かります。 \(f(0)=0, f(1)=1\) ですから、 \(\alpha=\frac{1+\sqrt{5}}{2},\beta=\frac{1-\sqrt{5}}{2}\) と置くと、 \(F(h)=\frac{1}{\sqrt{5}}((2-\beta)\alpha^h-(2-\alpha)\beta^h)\) です。 もし、\(h\) が十分に大きいなら、\(|\beta|\lt 1\) なので、 \(F(h)\approx\frac{2-\beta}{\sqrt{5}}\alpha^h\) となります(「\(\approx\)」は近似するの意味)。 \(n\) を高さが \(h\) のAVL木が含むノード数の最小値とすると、 \(n = f(h) = F(h)-1\) なので、 \(n+1\approx\frac{2-\beta}{\sqrt{5}}\alpha^h\) となり、最終的に \(h\approx\log_{\alpha}(n+1)+\log_{\alpha}\sqrt{5}-\log_{\alpha}(2-\beta)\) となります。 つまり、AVL木の最悪時の高さ \(h\) はノード数 \(n\) の対数に比例します。 ただし、\(n\) は十分に大きいとします。
ちなみに、\(\log_{\alpha}(n+1) はおよそ 1.44\log_2(n+1)\) なので、 AVL木は、高さが \(2\log_2(n+1)\) に比例する赤黒木より平衡が保たれていることになります。 また、完全2分木の高さは \(\log_2(n+1)\) に比例するので、 理想的なケースに比べるとバランスは崩れていることになります。
以下では、AVL木の仕組みを理解するためにたくさんの場合分けを行います。 気の短い人は場合分けの多さに挫折してしまうかもしれません。 今すぐAVL木を実装したいんだ。ぐずぐずしていられないんだという人は、 まとめ から読んでみてください。 AVL木は赤黒木に比べれば実装に必要な場合分けは簡単です。 後は図とサンプルコードを見ながら実装すれば大丈夫でしょう。
【挿入操作】
では、AVL木の挿入操作に関して詳しく見てみましょう。 AVL木に新たにノード挿入するには、まず2分探索木の要領で挿入します。 キーを検索し、 既にキーが存在すればそのノードを上書きします。存在しない場合、 木の末端まで行き着くので、そこに新しいノードを挿入しますが、 AVL木の場合は、挿入後、 木のバランスが崩れていれば回転を使って木を修正する必要があります。
新しいノードを挿入したらまず、 修正中であることを示すフラグである active フラグを True にして、 木の根の方向にさかのぼります。 そして、バイアスの値により分類し修正を行い、 注目している部分木のバランスを回復しAVL木に戻します。 修正後、注目している部分木の高さが挿入前より高いと、 さらに上位の木で修正が必要になるので active フラグを True にしてさかのぼります。 高さが変わらない場合は修正の必要はないので、 active フラグを False にしてさかのぼります。 一度 active フラグを False にしたらそれ以上は修正を行いません。 そのまま木の根までさかのぼり終了します。
それでは、具体的にバイアスによる分類の詳細を説明しましょう。 現在注目しているノードに u という名前を付けます。 まずは 「左部分木から active フラグが Trueでさかのぼって来た場合」 の処理です。 もともとはAVL木なので、-1 ≦ bias(u) ≦ 1 だったはずです。 そこにノードの挿入で左部分木が1つ高くなるので、 0 ≦ bias(u) ≦ 2 になります。 bias(u) = 2 ならバランスが崩れたので回転による修正が必要です。
< bias(u) = 0 の場合 >
右部分木の高さが高かったところに、 左部分木が1つ高くなった場合の処理です。 左右の部分木の高さが等しくなりますが、 u を根とする部分木の高さは変わりませんので、 上位の木で修正は必要ありません。 active フラグを False にしてさかのぼります。 バランスは崩れていないので回転は必要ありません。
< bias(u) = 1 の場合 >
左右の部分木の高さが等しかったところに、 左部分木が1つ高くなった場合の処理です。 u を根とする部分木の高さが1つ高くなるので、 上位の木でさらに修正が必要になります。 active フラグを True にしてさかのぼります。 バランスは崩れていないので回転は必要ありません。
< bias(u) = 2 の場合 >
左部分木が高かったところに、 さらに1つ左部分木が高くなった場合の処理です。分類のために u の左の子のことを v、v の右の子のことを w と呼ぶことにします。 まず大まかに u,v の状態の組で分類します。bias(u)=2 として、 v は bias(v)=1,bias(v)=-1,bias(v)=0 の3通りが考えられます。 なぜなら、v 以下の部分木はAVL木なので、 -1 ≦ bias(v) ≦ 1 だからです。 しかし、図を書いて考えると分かりますが、挿入の場合、 bias(v) = 0 のパターンはあり得ませんので除外されます。 bias(v) = -1 の場合、u,v だけでは情報が足りませんので w を追加する必要があります。従って bias(w)=1,bias(w)=-1,bias(w)=0 の3通りを考える必要があります。つまり全体では、 [bias(u)=2,bias(v)=1], [bias(u)=2,bias(v)=-1,bias(w)=1], [bias(u)=2,bias(v)=-1,bias(w)=-1], [bias(u)=2,bias(v)=-1,bias(w)=0] の4つのケースが考えられます。
CASE 1: [bias(u)=2,bias(v)=1]
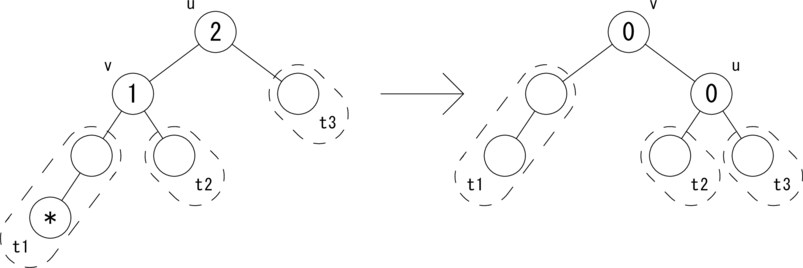
次の図のような関係が成り立つ場合に、木を rotateR(u) で回転して、左図を右図のように変形します。 ノードの中の数値はバイアス値を表しています。
|
'*' 付きのノードが挿入されたノードです。 それぞれの部分木で、|t2| = |t3| = h, |t1| = h + 1 という条件が成り立ちます。ここでは、 t1,t2,t3 が高さ 1 あるいは 2 の木として図示されていますが、 先の条件を満たせば、高さ h は任意です(h ≧ 0 とする)。 v を根とする部分木はAVL木になり、高さが元に戻ったので、 active フラグを False にしてさかのぼります。
CASE 2: [bias(u)=2,bias(v)=-1,bias(w)=1]
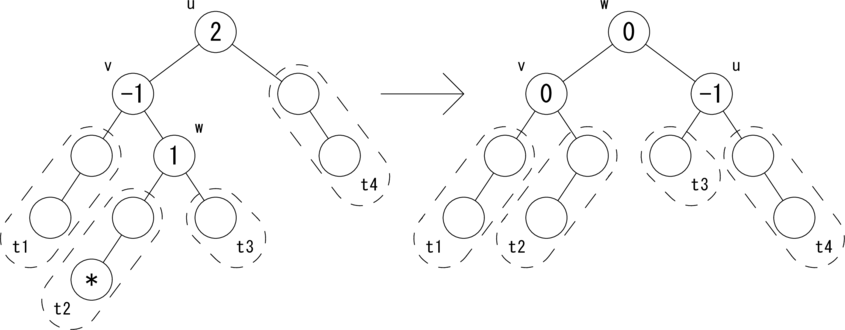
次の図のような関係が成り立つ場合に、木を rotateLR(u) で回転して、左図を右図のように変形します。
|
|t3| = h, |t1| = |t2| = |t4| = h + 1 が成り立ちます。 w を根とする部分木はAVL木となり、高さが元に戻ったので、 active フラグを False にしてさかのぼります。
CASE 3: [bias(u)=2,bias(v)=-1,bias(w)=-1]
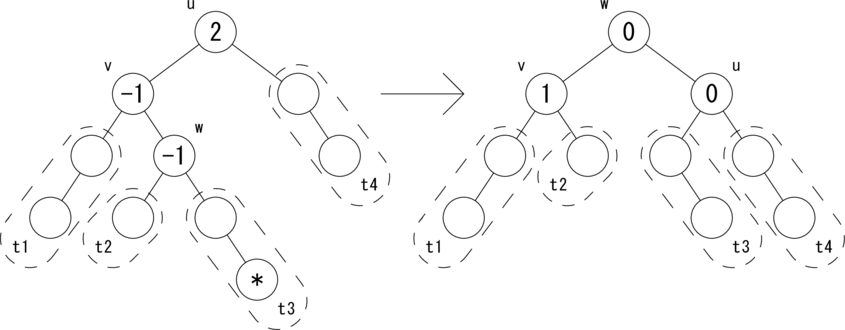
次の図のような関係が成り立つ場合に、木を rotateLR(u) で回転して、左図を右図のように変形します。
|
|t2| = h, |t1| = |t3| = |t4| = h + 1 が成り立ちます。 w を根とする部分木はAVL木となり、高さが元に戻ったので、 active フラグを False にしてさかのぼります。
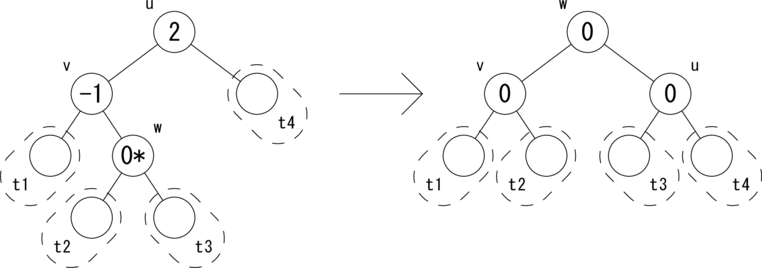
CASE 4: [bias(u)=2,bias(v)=-1,bias(w)=0]
次の図のような関係が成り立つ場合に、木を rotateLR(u) で回転して、左図を右図のように変形します。
|
t1 = t2 = t3 = t4 = 空の木(null または None)が成り立ちます。 w を根とする部分木はAVL木となり、高さが元に戻ったので、 active フラグを False にしてさかのぼります。
次は同じ挿入操作の 「右部分木から active フラグが True でさかのぼって来た場合」 の説明をしたいところですが、それは左右対称な処理になっていますので、 ひとまずおいておいて削除操作ついて説明します。
【削除操作】
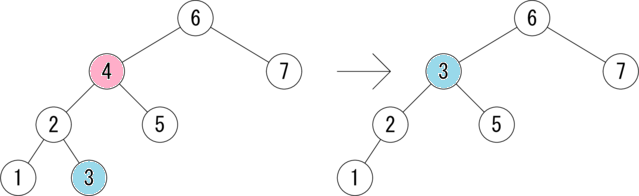
AVL木の削除を説明する前に、2分探索木の削除について簡単に説明します。 2分探索木でノードの削除を行うには、 削除したいノードが左端のノードの場合は、単にそのノードを削除し、 そのノードに右部分木があったのならそれを昇格させます。 また、削除したいノードが左部分木を持つ場合は、 左部分木の最大値のノードで削除したいノードを置き換え、 最大値だったノードを削除します。このとき、 削除したノードに左部分木があったのならそれを昇格させます。 以下に、2分探索木の削除の一例を具体的に示します。
|
図は、赤で示した 4 を削除する例を示しています。 4 には左部分木があります。そして、 4 の左部分木の最大値は 3 ですので、 4 を 3 で置き換え、元の 3 を削除します。 削除後も2分探索木の大小関係がうまく保たれていることが分かると思います。
AVL木の場合は、これに加え削除後、 木のバランスが崩れていれば回転を使って木を修正する必要があります。 ノードを削除したらまず、 変更の必要性を示すフラグである active フラグを True にして、 木の根の方向にさかのぼります。 そして、バイアスの値により分類し修正を行い、 注目している部分木のバランスを回復しAVL木に戻します。 修正後、注目している部分木の高さが削除前より低くなると、 さらに上位の木で修正が必要になるので active フラグを True にしてさかのぼります。 高さが変わらない場合は修正の必要はないので、 active フラグを False にしてさかのぼります。 一度 active フラグを False にしたらそれ以上は修正を行いません。 そのまま木の根までさかのぼり終了します。
それでは、具体的にバイアスによる分類の詳細を説明しましょう。 現在注目しているノードに u という名前を付けます。 まずは 「右部分木から active フラグが True でさかのぼって来た場合」 の処理です。 もともとはAVL木なので、-1 ≦ bias(u) ≦ 1 だったはずです。 そこにノードの削除で右部分木が1つ低くなるので、 0 ≦ bias(u) ≦ 2 になります。 bias(u) = 2 ならバランスが崩れたので回転による修正が必要です。
< bias(u) = 0 の場合 >
右部分木が高かったところで、 右部分木の高さが1つ低くなる場合の処理です。 左右の部分木の高さが等しくなり、 u を根とする部分木の高さが1つ低くなりますので、 上位の木で修正が必要になります。 active フラグを True にしてさかのぼります。 バランスは崩れていないので回転は必要ありません。
< bias(u) = 1 の場合 >
左右の部分木の高さが等しかったところで、 削除により右部分木の高さが1つ低くなる場合の処理です。 u を根とする部分木の高さは変わりませんので、 上位の木で修正は必要ありません。 active フラグを False にしてさかのぼります。 バランスは崩れていないので回転は必要ありません。
< bias(u) = 2 の場合 >
右部分木が低かったところに、 さらに1つ右部分木が低くなった場合の処理です。分類のために u の左の子のことを v、v の右の子のことを w と呼ぶことにします。 まず大まかに u,v の状態の組で分類します。bias(u) = 2 として、 v は bias(v)=1,bias(v)=-1,bias(v)=0 の3通りが考えられます。 なぜなら、v 以下の部分木はAVL木なので、 -1 ≦ bias(v) ≦ 1 だからです。 bias(v) = -1 の場合、u,v だけでは情報が足りませんので w を追加する必要があります。従って、bias(w)=1,bias(w)=-1,bias(w)=0 の3通りを考える必要があります。つまり全体では、 [bias(u)=2,bias(v)=1], [bias(u)=2,bias(v)=-1,bias(w)=1], [bias(u)=2,bias(v)=-1,bias(w)=-1], [bias(u)=2,bias(v)=-1,bias(w)=0], [bias(u)=2,bias(v)=0] の5つのケースが考えられます。
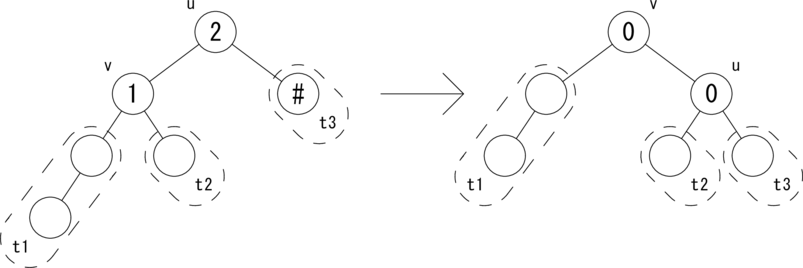
CASE 1: [bias(u)=2,bias(v)=1]
次の図のような関係が成り立つ場合に、 rotateR(u) で木を回転して、左図を右図のように変形します。 ノードの中の数値はバイアス値を表しています。
|
'#'
付きのノードかあるいはその子孫のノードが削除された結果、
右部分木の高さが1つ低くなったことを表しています。
それぞれの部分木で
|t2| = |t3| = h, |t1| = h + 1 という条件が成り立ちます。
ここでは、
t1,t2,t3 が高さ 1 あるいは 2 の木として図示されていますが、
先の条件を満たせば、高さ h は任意です(h ≧ 0 とする)。
v を根とする部分木はAVL木となり、高さが1つ低くなったので、
active フラグを True にしてさかのぼります。
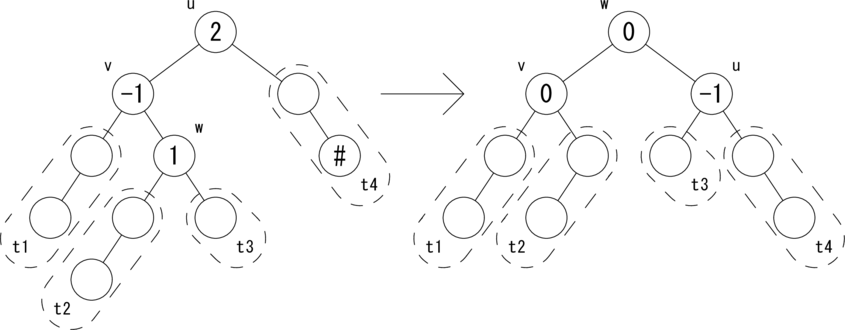
CASE 2: [bias(u)=2,bias(v)=-1,bias(w)=1]
次の図のような関係が成り立つ場合に、 rotateLR(u) で木を回転して、左図を右図のように変形します。
|
|t3| = h, |t1| = |t2| = |t4| = h + 1 が成り立ちます。 w を根とする部分木はAVL木となり、高さが1つ低くなったので、 active フラグを True にしてさかのぼります。
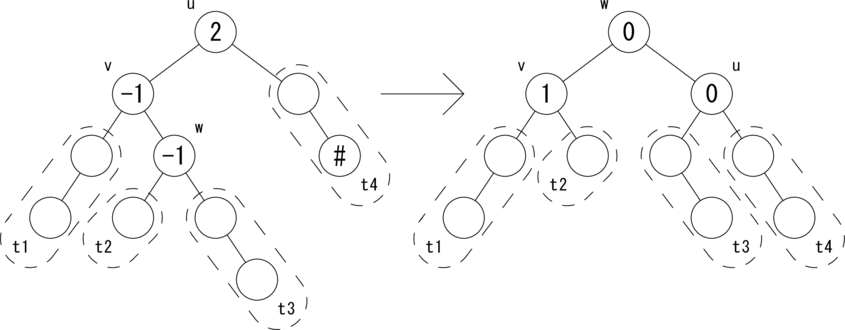
CASE 3: [bias(u)=2,bias(v)=-1,bias(w)=-1]
次の図のような関係が成り立つ場合に、 rotateLR(u) で木を回転して、左図を右図のように変形します。
|
|t2| = h, |t1| = |t3| = |t4| = h + 1 が成り立ちます。 w を根とする部分木はAVL木となり、高さが1つ低くなったので、 active フラグを True にしてさかのぼります。
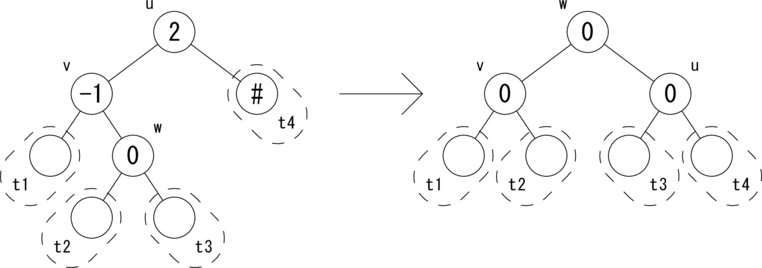
CASE 4: [bias(u)=2,bias(v)=-1,bias(w)=0]
次の図のような関係が成り立つ場合に、 rotateLR(u) 木を回転して、左図を右図のように変形します。
|
|t1| = |t2| = |t3| = |t4| = h が成り立ちます。 w を根とする部分木はAVL木となり、高さが1つ低くなったので、 active フラグを True にしてさかのぼります。
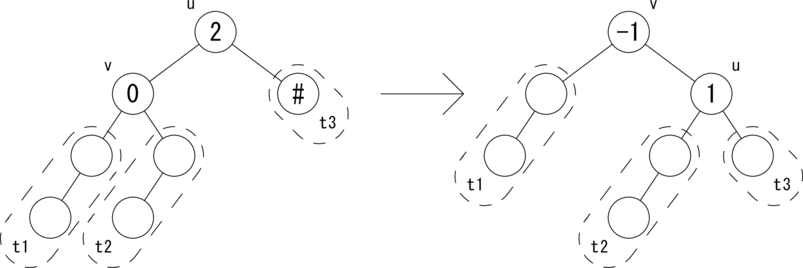
CASE 5: [bias(u)=2,bias(v)=0]
次の図のような関係が成り立つ場合に、 rotateR(u) で木を回転して、左図を右図のように変形します。
|
|t3| = h, |t1| = |t2| = h + 1 が成り立ちます。 v を根とする部分木はAVL木となり、高さは変わりませんので、 active フラグを False にしてさかのぼります。
【まとめ】
ここまで見てきて、 挿入操作と削除操作の類似点に気がついた人もいるかもしれません。 削除操作は CASE 5: [bias(u)=2,bias(v)=0] が余分にありますが、 それ以外の修正パターンは挿入操作と全く同じです。異なるのは、挿入操作が 「左部分木から active フラグが True でさかのぼって来た場合」 であるのに対して、削除操作では 「右部分木から active フラグが True でさかのぼって来た場合」 であることです。すなわち、 左部分木が高くなり過ぎた場合の処理は、 右部分木が低くなり過ぎた場合の処理と見ることができるということです。 active フラグに関しては、修正後に木の高さが変化する場合に True、 変化しない場合に False で統一することができます。
この性質をうまく使うとコーディングの時、 挿入操作のための修正処理と、 削除操作のための修正処理を共通にすることができます。
また、上記の場合分けは、AVL木の動作を理解するには必要ですが、 コーディング時にこれだけ細かい場合分けが必要なわけではありません。 注意して見ると、
- bias(u) = 2 のとき、bias(v) ≧ 0 ならば rotateR(u)、それ以外は rotateLR(u)
にまとめられます。
左右対称の処理なので詳細は省略しますが、
- bias(u) = -2 のとき、bias(v) ≦ 0 ならば rotateL(u)、それ以外は rotateRL(u)
にまとめられます(【コーディングの参考のための図】を参照のこと)。
サンプルコードでは _balanceL, _balanceR
で行われている処理です。
【コーディングの参考のための図】
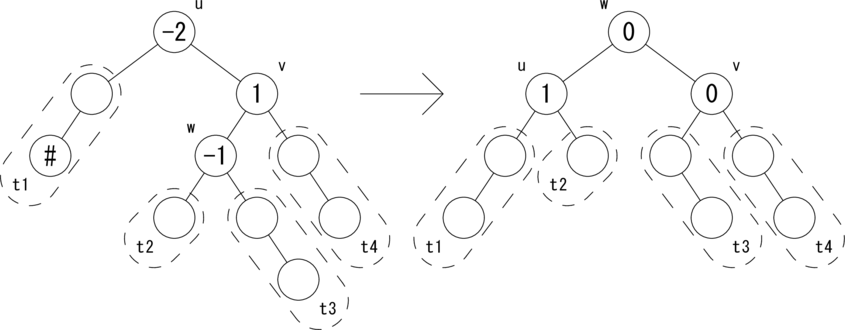
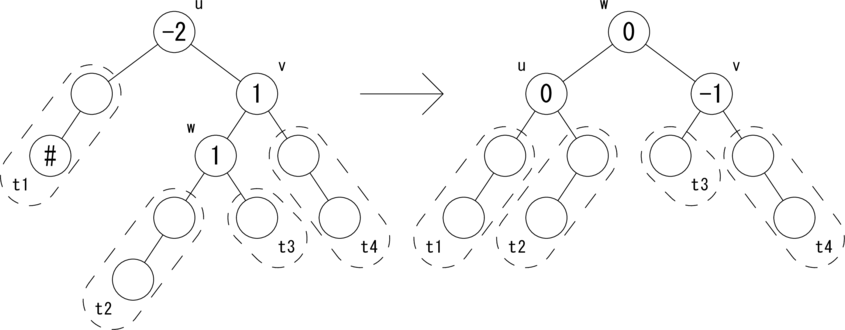
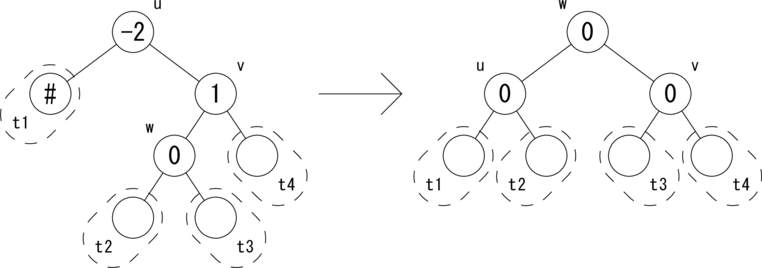
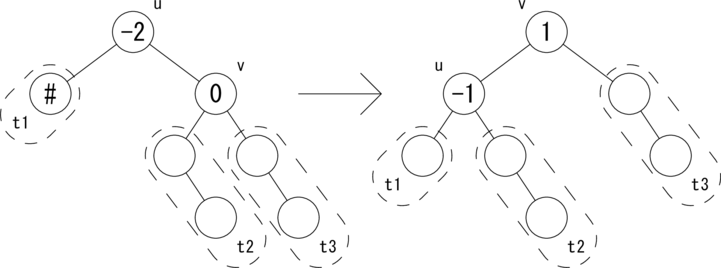
上では、挿入操作における 「左部分木から active フラグが True でさかのぼってきた場合」と、 削除操作における 「右部分木から active フラグが True でさかのぼってきた場合」 の処理を示しました。残りのパターンは左右対称なので詳細は省きます。 ただし、コーディングの参考のために図だけ示すこととします。 図示するのは 削除操作における「左部分木から active フラグが True でさかのぼってきた場合」 の bias(u) = -2 のケースです。
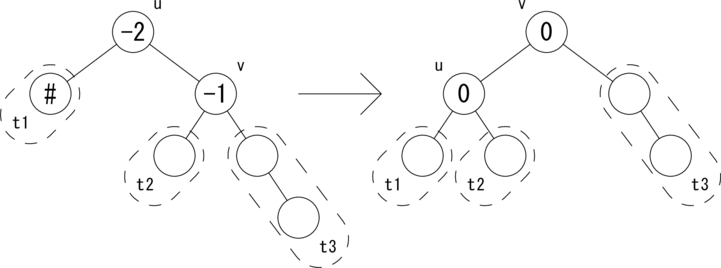
|
|
|
|
|
ところで、このページでも図が多用されていますが、 木のアルゴリズムの説明には図が欠かせません。 そこで、そのような図を描くためのツールを作りました。 興味のある方は、 こちらのページ をご覧ください。
【サンプルコード】
以下に、Java と Python によるAVL木のサンプルコードを示します。 タブになっていますので、目的の言語を選んでください。