B-Tree by Java & Python

【B木の定義】

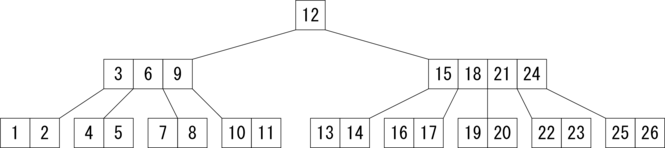
　それでは、B木に関して説明しましょう。以下の図で、 1,2 や 3,6,9 などが入っている箱のことをノードと言います。 ノードから出ている下側の線を枝と言います。 枝の先にあるノードのことを元のノードに対して子と言います。 子から見ると、元のノードを親と言います。 B木のノードは最大で m 本の枝を持ちます(m≧3)。 そして、枝と枝の間には要素が１つあります。つまり、 １つのノードに要素が最大で m - 1 個割り当てられることがあるわけです。 m のことをB木のオーダーと呼びます。

図2. B木の例(m = 5)

　B木は以下の条件を満たす多分探索木です。

• 各ノードは最大で m 本の枝を持つ(m≧3)
• 根と葉を除く各ノードは [m/2] 本以上の枝を持つ
• 枝と枝の間には要素が１つあり、各要素は昇順に整列されている
• 各ノードの左端の要素 a の左の枝の先には a より小さい要素がある
• 各ノードの右端の要素 a の右の枝の先には a より大きい要素がある
• 各ノードの要素 a, b (a < b) の間の枝の先には a より大きく b より小さい要素がある
• 全ての葉から根までのパス上のノード数は等しい

　B木の最後の条件は重要で、赤黒木やAVL木と違って、 B木が完全にバランスしていることを示しています。

　ここで、[m/2] は m/2 の小数点以下を切り上げる演算です。 m = 3 なら m/2 = 1.5 ですから [m/2] = 2 になります。 根(root)とは 12 が割り当てられている最上位のノードのことで、 葉とは空のノード(null または None)のことです。 1,2 や 4,5 が割り当てられているノードの下には本来は枝があるのですが、 簡略化のため図示はしていません。 空のノードはこれらの枝の先にあると考えます。 特定のノードを根と見なした木構造のことを部分木と言います。 最大の部分木はB木自身です。

【検索】

　B木で要素を検索するには、まず根から探し始めます。 例えば、図2.で 4 を探す場合、4 は 12 より小さいので、 左の部分木に含まれているはずです。そこで、左の枝の先のノードを調べます。 4 は 3 より大きく 6 より小さいので、 3 と 6 の間にある部分木に含まれているはずです。 そこで、3 と 6 の間の枝の先のノードを調べます。 すると、たどり着いたノードの中に 4 が見つかります。 もちろん、葉までたどり着いて目標の要素が見つからない場合もあります。 その場合は、B木に目標の要素は含まれていないことが分かります。

【挿入操作】

　では、B木の挿入操作について説明します。 赤黒木やAVL木同様まず要素が既に登録されているかどうか検索します。 既にあればその要素を置き換え、無ければ挿入することになります。 すなわち、挿入は常に最下層のノードで開始されます。

　挿入にはアクティブなノードを挿入します。アクティブなノードとは、 他のノードに触れると反応して木の形を変えるノードのことです。 挿入時のアクティブなノードは挿入する要素を１つ持ち、 部分木(枝)を２つ持ちます。 部分木は最初は空(null または None)です。

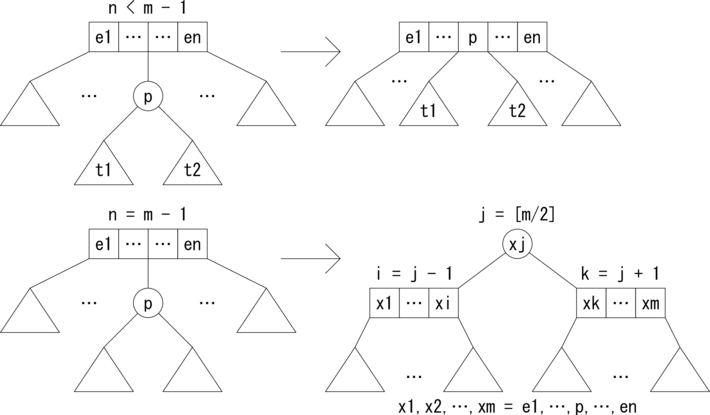
　図3.にB木の挿入パータンを示します。 通常のノードを四角で、アクティブなノードを丸で表しています。 p が挿入される要素です。三角は部分木を表しています。まず、 アクティブなノードの親ノードの要素数 n が n < m - 1 の場合ですが、 親ノードの要素と枝を１つ増やしてアクティブなノードを取り込みます。 アクティブなノードが無くなり安定します。

図3. B木の挿入パターン

　次に、アクティブなノードの親ノードの要素数 n が n = m - 1 の場合ですが、アクティブなノードを親ノードに取り込むと、 要素数が m、枝の数が m + 1 になり、B木の条件を満たさなくなります。 そこで親ノードをちょうど真ん中で分割し、アクティブなノードを生成します。 新たにアクティブなノードが生成されるので、 さらに上位のノードに対して挿入操作を再帰的に繰り返すことになります。 そして根までアクティブなノードが到達した場合は、 アクティブなノードを通常のノードに変換して新たな根にします。 説明が前後しますが、 空(null または None)のB木にノード挿入する場合も、 アクティブなノードを通常のノードに変換し根にします。

　図はたくさんある枝の特定の１本を処理する場合の例示になっています。 全てのパターンを列挙することは不可能だからです。 読者は個々の具体的ケースを想像で補う必要があります。 よく分からないという場合は、 2-3木のページ を参照してください。 2-3木はB木の m = 3 の場合です。2-3木のページでは、 2-3木の全ての挿入パターンを列挙してありますので、 これを手がかりに想像すると分かりやすいと思います。

　具体的な挿入の例を m = 3 のケースで示しておきましょう。 m = 3 なので [m/2] = 2 です。以下のようになります。

図4. B木の挿入の例(m = 3)

　左端において、赤で示したアクティブなノード 1 が挿入される例です。 ここでは、三角は null または None だと思ってください。 もちろん、部分木とみなすことも出来ます。 ノード 2,3 の要素数 n は 2 であり n = m - 1 なので、 アクティブなノードに触れると分割され、 新たにアクティブなノード 2 が生成されます。 2 は上位のノード 4 に挿入されることになります。 ノード 4 の要素数 n は 1 であり n < m - 1 なので、 アクティブなノードを取り込んで安定します。

　もう１つ、アクティブなノードが根に到達した場合の例をあげておきます。 アクティブなノードが根に到達した場合、 アクティブなノードをそのまま通常のノードに変換して新たな根にします。 このとき、木の高さが１段増えることになります。

図5. 挿入時のアクティブなノードが根に到達した場合(m = 3)

　気がついた人もいると思いますが、 B木の挿入では赤黒木やAVL木のような回転の操作がありません。 回転は部分木の高さを変えてしまうので木のバランスが変化します。 B木はバランスの状態を全く変えないので、 最初の木がバランスしていれば最後まで完全にバランスが取れています。 そして最初の木は空(null または None)ですから、 バランスは取れていると見なせます。 そのためB木は完全にバランスしているのです。

【削除操作】

　続いて、削除操作に関して説明します。 ただし、削除操作は最下層のノードで開始されるものと見なして説明します。 内部ノードでの削除も最下層のノードでの削除に帰着できるからです。 以下に内部ノードでの削除の一例を示します。

図6. 内部ノードでの削除の例

　赤で示した 7 の要素を削除するケースを示しています。 7 は最下層の要素ではないので左部分木があります。 そこで、青で示した左部分木の最大値 6 で 7 を置き換えます。 そして、元の 6 は削除します。 うまくB木の条件が維持されていることが分かると思います。 このように、内部ノードでの削除も最下層のノードでの削除に帰着できます。

　内部ノードでの削除の詳細は、 サンプルコード を読むことで代用してください。基本的な考え方は 赤黒木 や AVL木 と同じです。 口で説明しても混乱すると思いますので、 コードで確認するのが一番と思います。

　それでは、削除操作の詳細について説明しましょう。 始めに、[m/2] 本より多い枝を持つノードからの削除ですが、 これは単純に対象の要素と枝を削除することで完了です。 しかし、[m/2] 分岐のノードから要素と枝を削除すると、 枝の数が [m/2] - 1 になってB木の条件を満たさなくなります。 そこで、このノードを削除時のアクティブなノードと見なして木を変形します。

　変形の基本となる考え方はこうです。アクティブなノードと反応したら、 アクティブなノードの隣のノードから、余裕があれば、 つまり枝の数が [m/2] より多いノードだったら枝を１本分けてもらって、 アクティブなノードを [m/2] 分岐のノードに変換するというものです。 隣のノードに余裕がない場合、つまり枝の数が [m/2] だったら、 アクティブなノードと隣のノードを融合して、 m - 1 本以上 m 本以下の枝を持つノードに変換します。 このとき、親ノードで要素と枝が１つ減ることになるので、 場合によっては親ノードがアクティブなノードになります。 その場合、上位のノードで再帰的に変形を繰り返します。 そして、根がアクティブなノードになった場合、 枝の数が 2 以上であれば、そのまま通常のノードとして扱い、 要素が無く枝の数が 1 の分岐の無いノードになったら、 そのノードは余分なので切り詰めて、子ノードを新たな根にします。

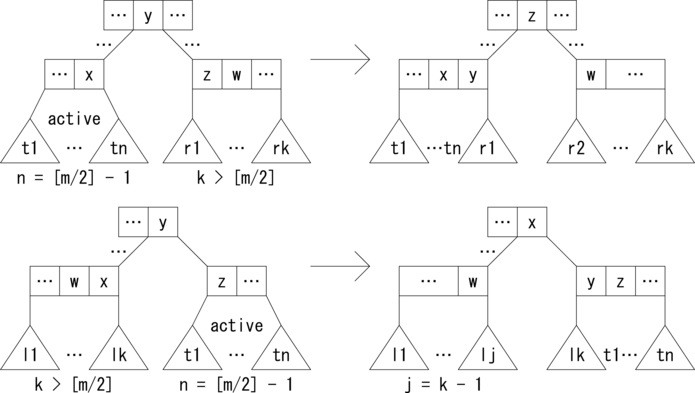
　まずは、 アクティブなノードの隣のノードに余裕がある場合の削除パターンを示します。 n = [m/2] - 1 のキャプションのノードがアクティブなノード、 k > [m/2] のキャプションのノードが余裕のある隣のノードです。 余裕のあるノードからアクティブなノードへ、枝を１本移動します。 これにより、アクティブなノードが通常のノードに変換されます。

図7. B木の削除パターン(隣に余裕がある場合)

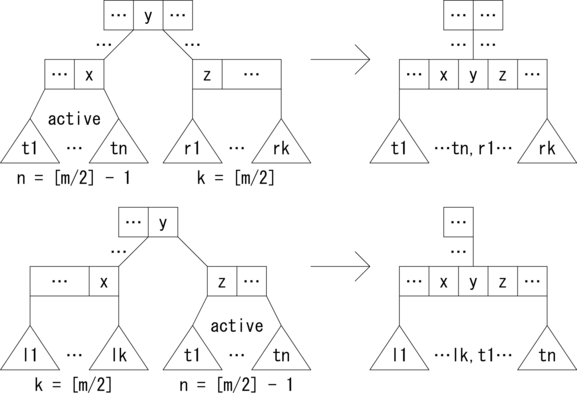
　次に、 アクティブなノードの隣のノードに余裕がない場合の削除パターンを示します。 n = [m/2] - 1 のキャプションのノードがアクティブなノード、 k = [m/2] のキャプションのノードが余裕のない隣のノードです。 アクティブなノードと余裕のないノードを融合して１つにします。 これにより、融合したノードは通常のノードに変換されます。 このとき、親ノードで要素と枝が１つ減るので、 親ノードがアクティブなノードになる可能性があることに注意してください。

図8. B木の削除パターン(隣に余裕がない場合)

　図はたくさんある枝の特定の２本を処理する場合の例示になっています。 全てのパターンを列挙することは不可能だからです。 読者は個々の具体的ケースを想像で補う必要があります。 よく分からないという場合は、 2-3木のページ を参照してください。 2-3木はB木の m = 3 の場合です。2-3木のページでは、 2-3木の全ての削除パターンを列挙してありますので、 これを手がかりに想像すると分かりやすいと思います。

　具体的な削除の例を m = 3 のケースで示しておきましょう。 m = 3 なので [m/2] = 2 です。以下のようになります。

図9. B木の削除の例(m = 3)

　左端の赤で示したノードがアクティブなノードです。 要素が１つしか無い最下層のノード(つまり、枝は２本)において、 要素の削除を行うと生成されます。 m = 3 なので、アクティブなノードには要素がなく、枝は１本です。 アクティブなノードの隣のノード 2 の枝の数 k は 2 であり k = [m/2] なので余裕がありません。そこで、アクティブなノードと融合します。 すると、ノード 1 から枝が１つ減り、新たにアクティブなノードになります。 今度は、隣のノード 5,7 の枝の数 k は 3 であり k > [m/2] なので余裕があります。そこで、ノード 5,7 から枝を１本分けてもらいます。 すると、アクティブなノードは無くなり安定します。

　もう１つ、アクティブなノードが根に到達した場合の例をあげておきます。 以下の図では、左端の赤いアクティブなノードが、 木の変形を繰り返して根に到達します。 m = 3 の場合は、アクティブなノードの枝の数は常に１つなので、 アクティブなノードは余分に伸びていることになります。 そこで、アクティブなノードを切り詰めて、子ノードを新たな根にします。 このとき、木の高さが１段低くなることになります。

図10. 削除時のアクティブなノードが根に到達した場合(m = 3)

　ところで、このページでも図が多用されていますが、 木のアルゴリズムの説明には図が欠かせません。 そこで、そのような図を描くためのツールを作りました。 興味のある方は、 こちらのページ をご覧ください。

【サンプルコード】

　以下に、Java と Python によるB木のサンプルコードを示します。 タブになっていますので、目的の言語を選んでください。

java python