2-3木
【これで分かった2-3木】
2-3木は、ファイルシステムやデータベースの実装の基礎となる B木 の最も簡単なケースです。
2-3木は平衡探索木の一種で、要素の検索・挿入・削除などの操作が、 いかなる場合でも O(log n) の計算量で行えます(n は要素数)。 何の工夫もしない単なる2分探索木では、 挿入や削除のパターンによっては木の茂り方のバランスが崩れてしまい、 各種操作に O(n) の計算量が必要になる場合があります。
2分探索木は、ノードが1つか2つの枝を持ちますが、 2-3木のノードは2つか3つの枝を持ちます。 そして、 赤黒木 や AVL木 のような平衡2分木が、 一応適度にバランスはしているものの完全にはバランスしていないのに対して、 2-3木は全ての葉から根までのパス上のノード数が等しく、 完全にバランスしています。 ここでは、2-3木の Java と Python による実装 を紹介します。
【2-3木の定義】
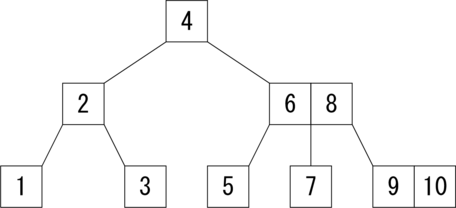
それでは、2-3木に関して説明しましょう。2-3木とは2分探索木の親戚です。 具体的に示すと図1.のようになります。 図1.で 4 や 6,8 などが入っている箱をノードと言います。 2分探索木のノードが1つか2つの枝を持っているのに対して、 2-3木では2つか3つの枝をちます。 そして、枝と枝の間には要素が1つあります。 つまり、1つのノードに要素が2つ割り当てられることがあるわけです。
|
図1.で 6,8 を要素に持つノードに注目してください。 6 より小さい 5 は左に枝に、6 と 8 の間の 7 は真ん中の枝に、 8 より大きい 9,10 は右の枝に配置されています。 2分探索木の簡単な拡張になっていることが分かると思います。
ここで、根(root)とは 4 が割り当てられている最上位のノードのことです。
また、葉とは空のノード(null または None)のことです。
1 や 9,10 が割り当てられているノードの下には本来枝があるのですが、
簡略化のため図示はしていません。
空のノードはこれらの枝の先にあると考えます。
特定のノードを根と見なした木構造のことを部分木と言います。
最大の部分木は2-3木自身です。
そして忘れてはならない重要な性質があります。それは、 全ての葉から根までのパス上のノード数は等しい ということです。 赤黒木やAVL木では木のバランスは完全には取れていませんでしたが、 2-3木では完全にバランスしていることになります。
2-3木とは以下の条件を満たす平衡探索木です。
- 各ノードは2本以上で3本以下の枝を持つ
- 枝と枝の間には要素が1つあり、各要素は昇順に整列している
- 各ノードの左端の要素 a の左の枝の先には a より小さい要素がある
- 各ノードの右端の要素 a の右の枝の先には a より大きい要素がある
- 各ノードの要素 a, b (a < b) の間の枝の先には a より大きく b より小さい要素がある
- 全ての葉から根までのパス上のノード数は等しい
【検索】
図1.を例に、要素 7 を検索する方法を説明しましょう。 検索はまず、根から開始されます。図1.では 4 のノードです。 7 は 4 より大きいので、4 の右の部分木に含まれているはずです。 そこで、右の部分木を調べます。右の部分木の根には 6,8 が含まれています。 7 は 6 よりも大きく 8 より小さいので、 6 と 8 の間の部分木に含まれているはずです。 そこで、6 と 8 の間の部分木を調べると 7 が見つかります。 もちろん、葉までたどり着いて目標の要素が見つからない場合もあります。 その場合は、2-3木に目標の要素は含まれていないことが分かります。
【挿入操作】
では、2-3木の挿入操作について説明します。 赤黒木やAVL木同様まず要素が既に登録されているかどうか検索します。 既にあればその要素を置き換え、無ければ挿入することになります。 すなわち、挿入は常に最下層のノードで開始されます。
挿入にはアクティブなノードを挿入します。アクティブなノードとは、
他のノードに触れると反応して木の形を変えるノードのことです。
挿入時のアクティブなノードは挿入する要素を1つ持ち、
部分木(枝)を2つ持ちます。部分木は最初は空(null または None)です。
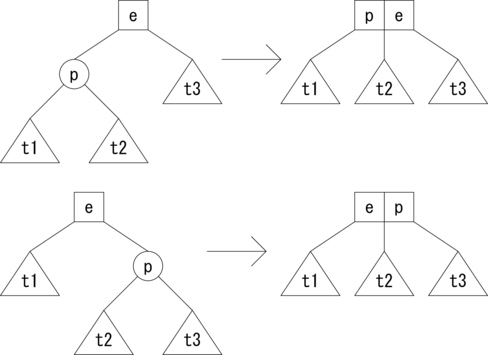
まず、親ノードが2分岐の場合の挿入操作のパターンを図2.に示します。 通常のノードを四角で、アクティブなノードを丸で表しています。 p が挿入される要素です。三角は部分木を表しています。 アクティブなノードが親ノードと反応して3分岐のノードになり安定します。
|
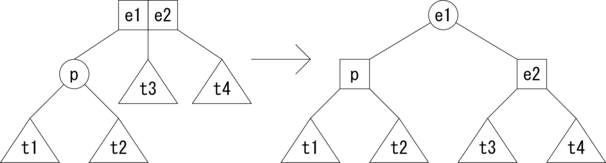
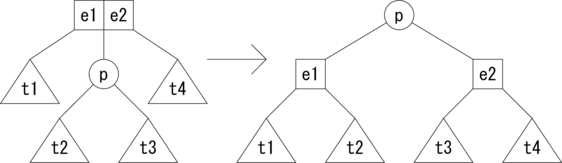
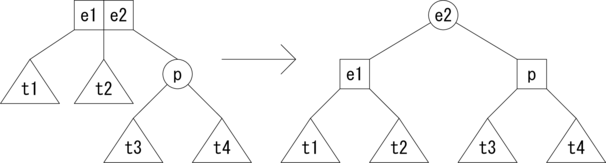
次に、親ノードが3分岐の場合の挿入操作のパターンを図3.に示します。 親ノードが分割され2分岐のノードが新たに3つ生成されます。 1つはアクティブなノードで、残りの分割されたノードを子に持ちます。
|
|
|
新たにアクティブなノードが生成されるので、 さらに上位のノードに対して挿入操作を再帰的に繰り返すことになります。 そして根までアクティブなノードが到達した場合は、 アクティブなノードを通常のノードに変換して新たな根にします。 説明が前後しますが、空の2-3木にノード挿入する場合も、 アクティブなノードを通常のノードに変換し根にします。
これらの処理は、サンプルコードでは
balance2Li, balance2Ri, balance3Li, balance3Mi, balance3Ri
で行われている処理です。
ここで、具体的な挿入の例を示しておきましょう。以下のようになります。

|
左端において、赤で示したアクティブなノード 1 が挿入される例です。
ここでは、三角は null または None だと思ってください。
もちろん、部分木とみなすことも出来ます。
アクティブなノードの親ノード 2,3 は3分岐なので、
アクティブなノードに触れると分割され、
新たにアクティブなノード 2 が生成されます。
ノード 2 は親ノード 4 に挿入されることになります。
ノード 4 は2分岐なので、アクティブなノードを取り込んで安定します。
もう1つ、アクティブなノードが根に到達した場合の例をあげておきます。 アクティブなノードが根に到達した場合、 アクティブなノードをそのまま通常のノードに変換して新たな根にします。 このとき、木の高さが1段増えることになります。

|
気がついた人もいると思いますが、 2-3木の挿入では赤黒木やAVL木のような回転の操作がありません。 回転は部分木の高さを変えてしまうので木のバランスが変化します。 2-3木はバランスの状態を全く変えないので、 最初の木がバランスしていれば最後まで完全にバランスが取れています。 そして最初の木は空ですから、バランスは取れていると見なせます。 そのため2-3木は完全にバランスしているのです。
【削除操作】
次に、削除操作について説明します。 ただし、削除操作は最下層のノードで開始されるものと見なして説明します。 内部ノードでの削除も最下層のノードでの削除に帰着できるからです。 内部ノードでの削除の具体的な説明はコードを読むことで代用してください。 基本的考え方は 赤黒木 や AVL木 と同じですが、 ノードが3分岐のときの処理が少し複雑です。 口で説明しても混乱すると思いますので、 コードで確認するのが一番と思います。
以下に内部ノードでの削除の一例を示します。

|
赤で示した 7 の要素を削除するケースを示しています。 7 は最下層の要素ではないので左部分木があります。 そこで、青で示した左部分木の最大値 6 で 7 を置き換えます。 そして、元の 6 は削除します。 うまく2-3木の条件が維持されていることが分かると思います。 このように、内部ノードでの削除も最下層のノードでの削除に帰着できます。
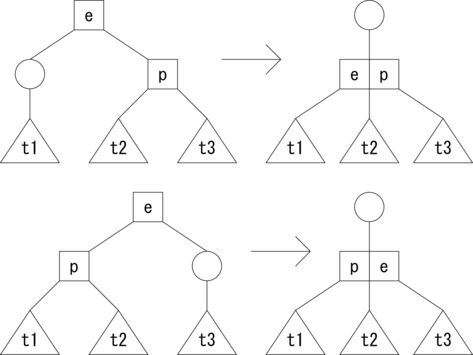
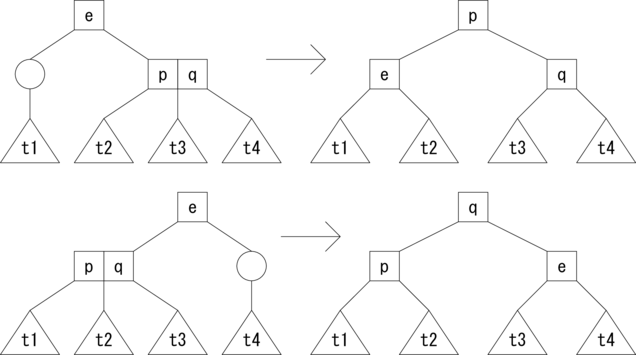
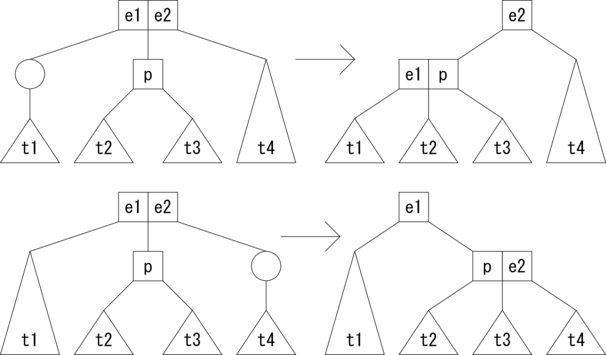
さて、まずは3分岐のノードからの削除ですが、 これは単純に対象の要素と枝を削除して2分岐のノードにすることで完了です。 しかし、2分岐のノードから要素と枝を削除すると、 要素が無く枝が1つのノードになってしまって2-3木ではなくなります。 そこで、 この枝が1つのノードを削除時のアクティブなノードと見なして木を変形します。
削除のパターンはたくさんありますが、 基本となる考え方は全部同じです。それは、アクティブなノードと反応したら、 アクティブなノードの隣のノードから、余裕があれば、 つまり3分岐のノードだったら枝を1本分けてもらって、 アクティブなノードを2分岐のノードに変換するというものです。 隣のノードに余裕がない場合、つまり2分岐のノードだったら、 アクティブなノードと隣のノードを融合して3分岐のノードに変換します。 このとき、親ノードで枝が1つ減ることになるので、 場合によっては親ノードがアクティブなノードになります。 その場合、再帰的に上位のノードで変形を繰り返します。 そして、根がアクティブなノードになった場合は、 そのノードは余分なので切り詰めて、子ノードを新たな根にします。
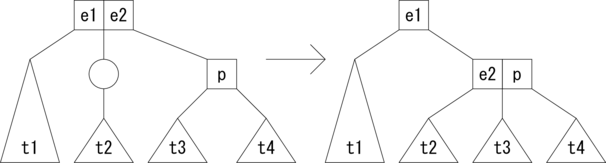
それではまず、親ノードが2分岐の場合の削除パターンを示します。 通常のノードを四角で、アクティブなノードを丸で表します。 三角は部分木を表しています。
|
|
続いて、親ノードが3分岐の場合の削除パターンを示します。
|
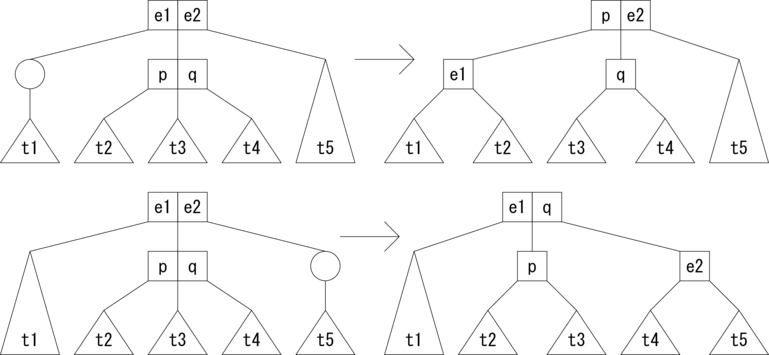
|
|
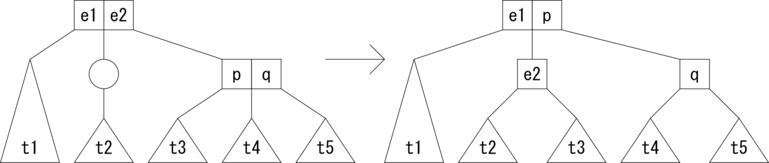
|
これらの処理は、サンプルコードでは
balance2Ld, balance2Rd, balance3Ld, balance3Md, balance3Rd
で行われている処理です。
ここで、具体的な削除の例を示しておきましょう。以下のようになります。

|
左端の赤で示したノードがアクティブなノードです。 要素が1つしか無い最下層のノードにおいて、 要素の削除を行うと生成されます。 アクティブなノードには要素がなく、枝は1本です。 アクティブなノードの隣のノード 2 は2分岐なので余裕がありません。 そこで、アクティブなノードと融合します。 すると、ノード 1 から枝が1つ減り、新たにアクティブなノードになります。 今度は、隣のノード 5,7 は3分岐なので余裕があります。 そこで、ノード 5,7 から枝を1本分けてもらいます。 すると、アクティブなノードは無くなり安定します。
もう1つ、アクティブなノードが根に到達した場合の例をあげておきます。 アクティブなノードの枝の数は1つなので、 余分に伸びていることになります。 そこで、アクティブなノードを切り詰めて、子ノードを新たな根にします。 このとき、木の高さが1段低くなることになります。

|
【サンプルコード】
2-3木の Java と Python による実装は以下のようになります。 タブになっていますので、目的の言語を選んでください。 Java のコードは速度を考えて new を減らした実装にしてあります。 Python のコードは速度のことは気にせずに、 分かりやすさ優先で実装してあります。