赤黒木ソートの他にも、最悪計算量が \(O(n\log n)\) の平衡木を使った ツリーソート(2分木ソート, tree sort) はあります。その1つがAVL木ソートです。
AVL木(AVL Tree)は赤黒木より厳密に平衡性を維持しようとしますので、 一般には赤黒木より遅いと言われています。しかし、Haskell でツリーソートを 実装する限りにおいては、AVL木を使ったツリーソートの方が高速です。
ここでは、Haskell でAVL木を使ったツリーソートを実装してみましょう。 もちろん、AVL木を使ったツリーソートも安定ソートです。Haskell による AVL木を使ったツリーソートの実装は以下のようになります。 C++ による実装をお望みの方は こちらのページ へどうぞ。
AVL木は、左右の部分木の高さの差が1以内に保たれた平衡木です。もし バランスが崩れて左右の高さの差が2になったら木を回転という操作で変形して 再び高さの差が1以内になるように修正します。具体的には以下のようになり ます。

|
回転後も2分探索木の各ノードの大小関係がうまく保たれていることが分かる
と思います。これを実現するために上記のコードの insertBy
関数に回転操作を実装してあります。以下では insert(挿入操作) の
動作を説明します。
AVL木に新たにノード挿入するには、まず2分探索木の要領で挿入します。 キーを検索し、 既にキーが存在すればそのノードを上書きします。存在しない場合、 木の最下層まで行き着くので、そこに新しいノードを挿入しますが、 AVL木の場合は、挿入後、 木のバランスが崩れていれば回転を使って木を修正する必要があります。
木の各ノードには左右の部分木の状態を示す値が割り当てられており、 左部分木が高い状態を L、右部分木が高い状態を R、 左右の部分木の高さが等しい状態を E と表します。 この情報をもとにパターンマッチを行い、 木の形と {L,E,R} の状態の修正を行います。
新しいノードを挿入したらまず、 変更の必要性を示すフラグである Change フラグを True にして、 木の根(root)の方向にさかのぼります。 そして、パターンマッチでパターン毎の修正を行います。 修正後、注目している部分木の高さが1つ高くなると、 さらに上位の木で修正が必要になるので Change フラグを True にしてさかのぼります。 高さが変わらない場合は修正の必要はないので、 Change フラグを False にしてさかのぼります。 一度 Change フラグを False にしたらそれ以上は修正を行いません。 そのまま木の根(root)までさかのぼり終了します。
それでは、具体的にパターンマッチの詳細を説明しましょう。 現在注目しているノードに u という名前を付けます。 まずは「左部分木から Change フラグが True でさかのぼって来た場合」の処理です。u の状態によって処理を分けます。
左右の部分木の高さが等しかったところに、 左からさかのぼって来るのですから、 左部分木の高さが1つ高くなります。 また、u を根とする部分木の高さも1つ高くなります。 u を根とする部分木の高さが1つ高くなるということは、 上位の木でさらに修正が必要になるということです。 u の状態を L に、Change フラグを True にしてさかのぼります。
右部分木が高かったところに、左からさかのぼって来るのですから、 左右の部分木の高さが等しくなります。 また、u を根とする部分木の高さは変わりませんので、 さらに上位の木では修正は必要ないということです。 u の状態を E に、Change フラグを False にしてさかのぼります。
左部分木が高かったところに、 左からさかのぼって来た場合の処理です。パターンマッチのために、 u の左の子のことを v、v の右の子のことを w と呼ぶことにします。 まず大まかに u,v の状態の組で分類します。u は L ですので、 (u=L,v=L),(u=L,v=R),(u=L,v=E) の3通りが考えられます。しかし、 図を書いて考えると分かりますが、挿入の場合、 (u=L,v=E) のパターンはあり得ませんので除外されます。 v が R の場合、u,v だけでは情報が足りませんので w を追加する必要があります。従って v が R の場合、 (u=L,v=R,w=L),(u=L,v=R,w=R),(u=L,v=R,w=E) の3通りを考える必要があります。つまり全体では、 (u=L,v=L),(u=L,v=R,w=L),(u=L,v=R,w=R),(u=L,v=R,w=E) の4つのケースが考えられます。
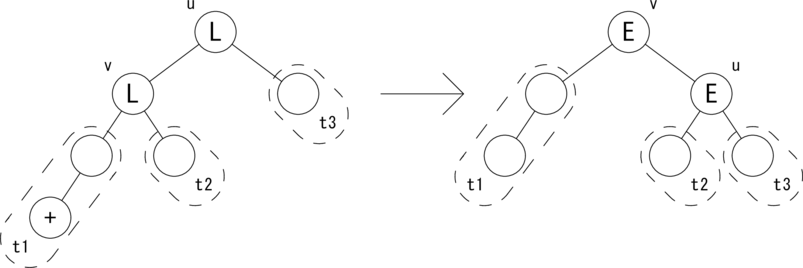
次の図のような関係が成り立つ場合に木を回転して、 左図を右図のように変形します。
|
'+' 付きのノードが挿入されたノードです。
木 t の高さを |t| と表すと、|t2| = |t3| = h, |t1| = h + 1
という条件が成り立ちます。ここでは、
t1,t2,t3 が高さ 1 あるいは 2 の木として図示されていますが、
先の条件を満たせば、高さ h は任意です(h ≧ 0 とする)。
ノードの状態 {L,E,R} も変形後に合わせて変更します。
バランスが復活し、v を根とする部分木の高さが元に戻ったので、
Change フラグを False にしてさかのぼります。
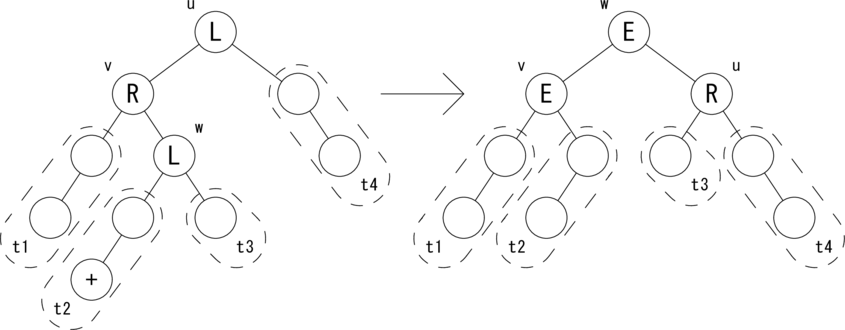
次の図のような関係が成り立つ場合に木を回転して、 左図を右図のように変形します。
|
|t3| = h, |t1| = |t2| = |t4| = h + 1 が成り立ちます。 ノードの状態 {L,E,R} を変形後に合わせて変更します。 バランスが復活し、w を根とする部分木の高さが元に戻ったので、 Change フラグを False にしてさかのぼります。
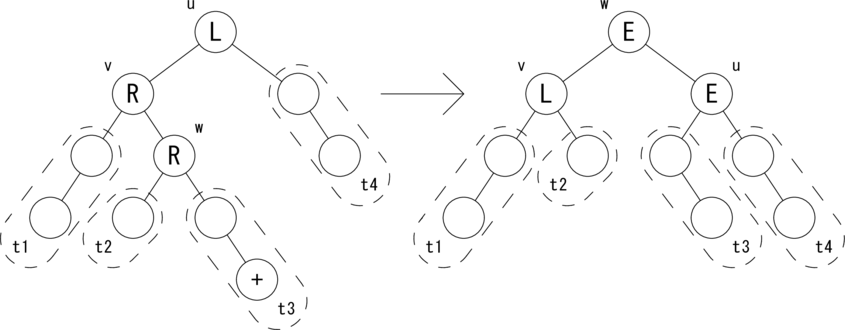
次の図のような関係が成り立つ場合に木を回転して、 左図を右図のように変形します。
|
|t2| = h, |t1| = |t3| = |t4| = h + 1 が成り立ちます。 ノードの状態 {L,E,R} を変形後に合わせて変更します。 バランスが復活し、w を根とする部分木の高さが元に戻ったので、 Change フラグを False にしてさかのぼります。
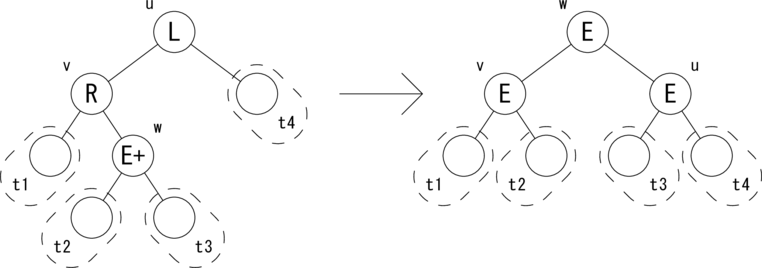
次の図のような関係が成り立つ場合に木を回転して、 左図を右図のように変形します。
|
t1 = t2 = t3 = t4 = Empty が成り立ちます。ノードの状態 {L,E,R} を変形後に合わせて変更します。 バランスが復活し、w を根とする部分木の高さが元に戻ったので、 Change フラグを False にしてさかのぼります。
次は挿入操作の 「右部分木から Change フラグが True でさかのぼって来た場合」 の説明をしたいところですが、 それは左右対称なパターンマッチになっていますので省略します。
さて、AVL木と言えばソートに使うというより、マップを実装するデータ構造 として有名です。せっかくAVL木を使ったのですから、 delete(削除操作) の処理も含んだマップの実装も見てみましょう。 以下のようになります。Java による実装をお望みの方は このリンク からどうぞ。
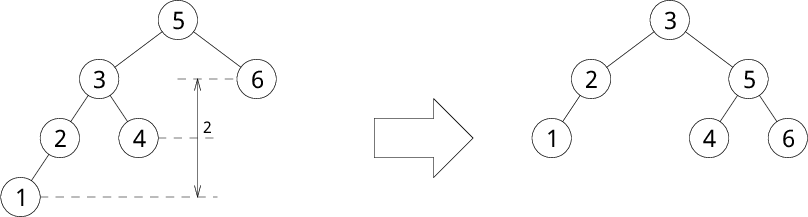
まず、AVL木の削除を説明する前に、 2分探索木の削除について簡単に説明します。 2分探索木でノードの削除を行うには、 削除したいノードが左端のノードの場合は、単にそのノードを削除し、 そのノードに右部分木があったのならそれを昇格させます。 また、削除したいノードが左部分木を持つ場合は、 左部分木の最大値のノードで削除したいノードを置き換え、 最大値だったノードを削除します。このとき、 削除したノードに左部分木があったのならそれを昇格させます。 以下に、2分探索木の削除の一例を具体的に示します。
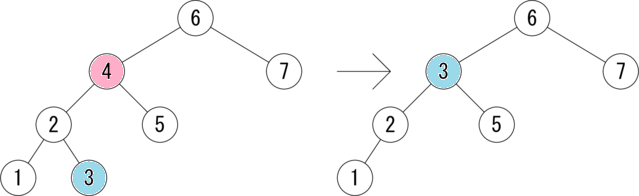
|
図は、赤で示した 4 を削除する例を示しています。 4 には左部分木があります。そして、 4 の左部分木の最大値は 3 ですので、 4 を 3 で置き換え、元の 3 を削除します。 削除後も2分探索木の大小関係がうまく保たれていることが分かると思います。
これに加えAVL木の場合は、削除後、 木のバランスが崩れていれば回転を使って木を修正する必要があります。 ノードを削除したらまず、 変更の必要性を示すフラグである Change フラグを True にして、 木の根(root)の方向にさかのぼります。 そして、パターンマッチでパターン毎の修正を行います。 修正後、注目している部分木の高さが1つ低くなると、 さらに上位の木で修正が必要になるので Change フラグを True にしてさかのぼります。 高さが変わらない場合は修正の必要はないので、 Change フラグを False にしてさかのぼります。 一度 Change フラグを False にしたらそれ以上は修正を行いません。 そのまま木の根(root)までさかのぼり終了します。
それでは、具体的にパターンマッチの詳細を説明しましょう。 現在注目しているノードに u という名前を付けます。 まずは「右部分木から Change フラグが True でさかのぼって来た場合」の処理です。u の状態によって処理を分けます。
左右の部分木の高さが等しかったところで、 削除により右部分木の高さが1つ低くなります。 しかし、u を根とする部分木の高さは変わりませんので、 上位の木で修正は必要ありません。 u の状態を L に、Change フラグを False にしてさかのぼります。
右部分木が高かったところで、 右部分木の高さが1つ低くなるのですから、 左右の部分木の高さが等しくなります。 そして、u を根とする部分木の高さも1つ低くなりますので、 上位の木でさらに修正が必要になります。 u の状態を E に、Change フラグを True にしてさかのぼります。
左部分木が高かったところに、 右からさかのぼって来た場合の処理です。パターンマッチのために、 u の左の子のことを v、v の右の子のことを w と呼ぶことにします。 まず大まかに u,v の状態の組で分類します。u は L ですので、 (u=L,v=L),(u=L,v=R),(u=L,v=E) の3通りが考えられます。 v が R の場合、u,v だけでは情報が足りませんので w を追加する必要があります。従って v が R の場合、 (u=L,v=R,w=L),(u=L,v=R,w=R),(u=L,v=R,w=E) の3通りを考える必要があります。つまり全体では、 (u=L,v=L),(u=L,v=R,w=L),(u=L,v=R,w=R),(u=L,v=R,w=E),(u=L,v=E) の5つのケースが考えられます。
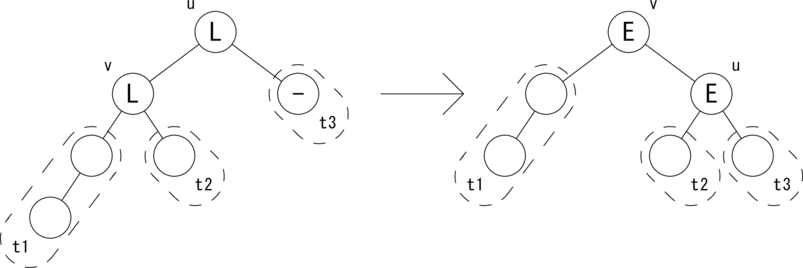
次の図のような関係が成り立つ場合に木を回転して、 左図を右図のように変形します。
|
'-'
付きのノードかあるいはその子孫のノードが削除された結果、
右部分木の高さが1つ低くなったことを表しています。ここで、
|t2| = |t3| = h, |t1| = h + 1 という条件が成り立ちます。
ノードの状態 {L,E,R} も変形後に合わせて変更します。
バランスが復活し、v を根とする部分木の高さが1つ低くなったので、
Change フラグを True にしてさかのぼります。
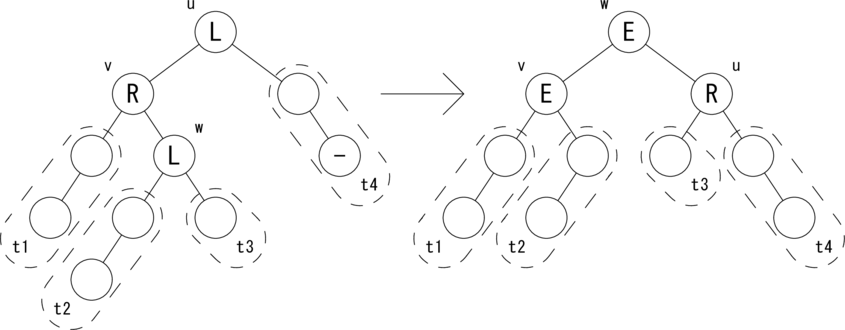
次の図のような関係が成り立つ場合に木を回転して、 左図を右図のように変形します。
|
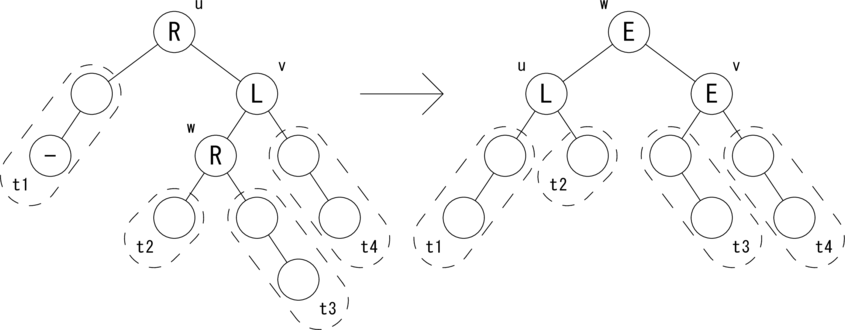
|t3| = h, |t1| = |t2| = |t4| = h + 1 が成り立ちます。 ノードの状態 {L,E,R} を変形後に合わせて変更します。 バランスが復活し、w を根とする部分木の高さが1つ低くなったので、 Change フラグを True にしてさかのぼります。
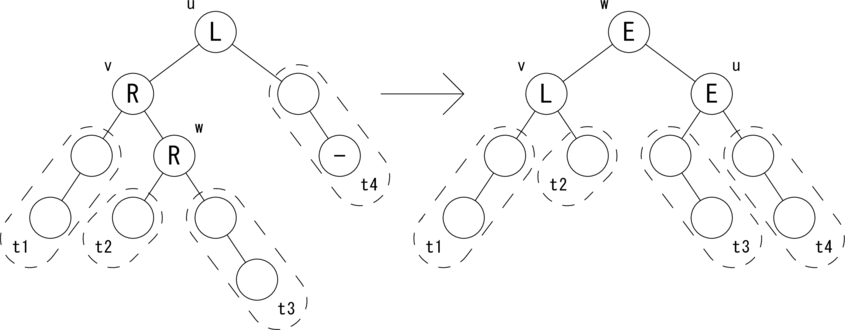
次の図のような関係が成り立つ場合に木を回転して、 左図を右図のように変形します。
|
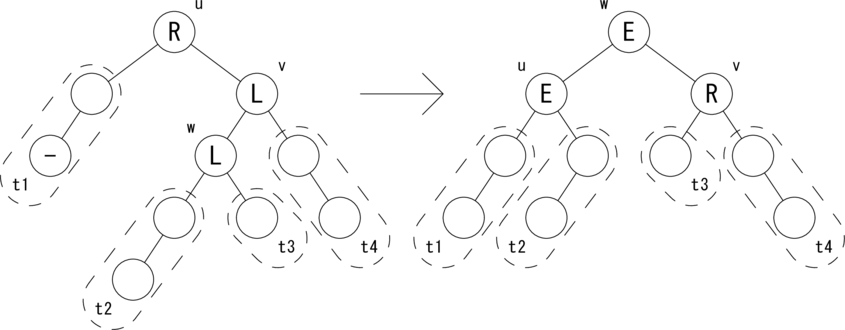
|t2| = h, |t1| = |t3| = |t4| = h + 1 が成り立ちます。 ノードの状態 {L,E,R} を変形後に合わせて変更します。 バランスが復活し、w を根とする部分木の高さが1つ低くなったので、 Change フラグを True にしてさかのぼります。
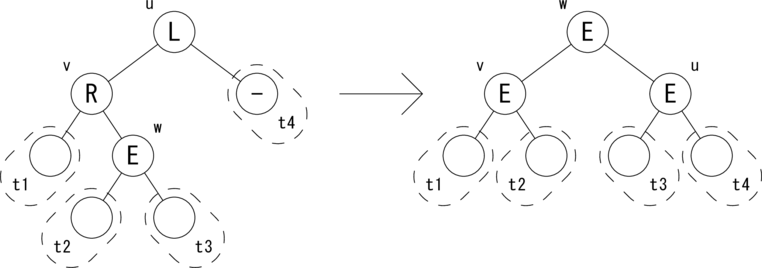
次の図のような関係が成り立つ場合に木を回転して、 左図を右図のように変形します。
|
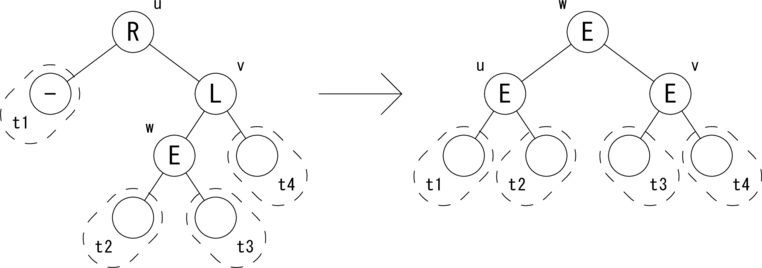
|t1| = |t2| = |t3| = |t4| = h が成り立ちます。 ノードの状態 {L,E,R} を変形後に合わせて変更します。 バランスが復活し、w を根とする部分木の高さが1つ低くなったので、 Change フラグを True にしてさかのぼります。
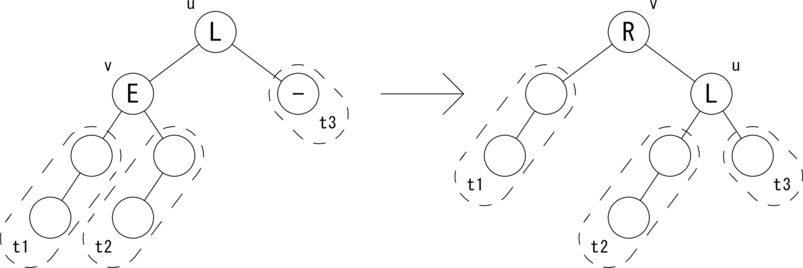
次の図のような関係が成り立つ場合に木を回転して、 左図を右図のように変形します。
|
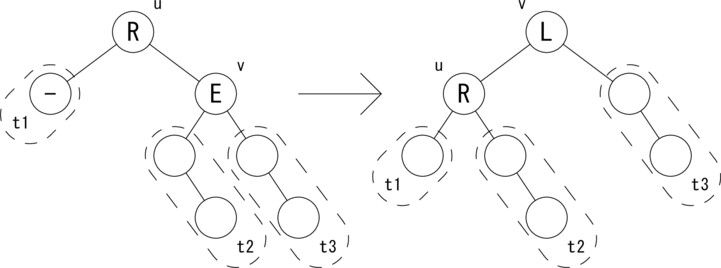
|t3| = h, |t1| = |t2| = h + 1 が成り立ちます。 ノードの状態 {L,E,R} を変形後に合わせて変更します。 バランスが復活し、v を根とする部分木の高さは変わりませんので、 Change フラグを False にしてさかのぼります。
ここまで見てきて、 挿入操作と削除操作の類似点に気がついた人もいるかもしれません。 削除操作は CASE 5: (u=L,v=E) が余分にありますが、 それ以外の修正パターンは挿入操作と全く同じです。異なるのは、挿入操作が 「左部分木から Change フラグが True でさかのぼって来た場合」 のパターンマッチであるのに対して、削除操作では 「右部分木から Change フラグが True でさかのぼって来た場合」 のパターンマッチであることです。すなわち、 左部分木が高くなり過ぎた場合の処理は、 右部分木が低くなり過ぎた場合の処理と見ることができるということです。 また、 それぞれの処理の Change フラグ変更時の True と False が逆になっています。
この性質をうまく使うとコーディングの時、 挿入操作のためのパターンマッチと、 削除操作のためのパターンマッチを共通にすることができます。
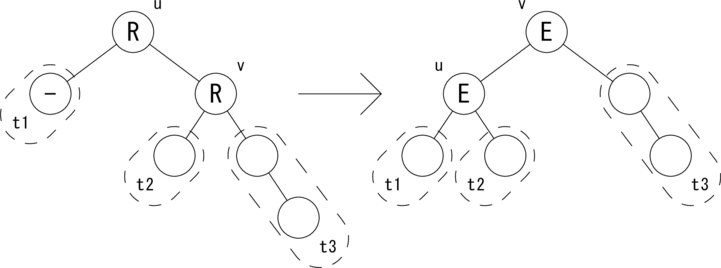
上では、挿入操作における 「左部分木から Change フラグが True でさかのぼってきた場合」と、 削除操作における 「右部分木から Change フラグが True でさかのぼってきた場合」 の処理を示しました。残りのパターンは左右対称なので説明は省きます。 ただし、コーディングの参考のために図だけ示すこととします。 図示するのは削除操作における 「左部分木から Change フラグが True でさかのぼってきた場合」 の u が R のケースです。
|
|
|
|
|